Ostrosłup Esssssa: Dany jest ostrosłup prawidłowy trójkątny ABCS o podstawie ABC i wierzchołku S. Objętość tego ostrosłupa jest równa 72, a promień okręgu opisanego na podstawie ABC jest równy 2. Oblicz sinus kąta między wysokością tego ostrosłupa i jego ściana boczną. proszę o pomoc

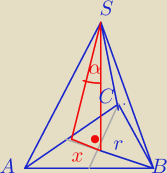
janek191: V = 72 r = 2 x = 1

	√3
h = 3 ⇒ a		= 3
	2

a = 2 √3

	a2√3
PΔ =		= 3√3
	4

	1
V =		Pp*H = √3*H = 72
	3

H = 24√3 (h_b)² = x² + H² = 1 + 1728 = 1729

	x		1
sin α =		=
	hb		√1729

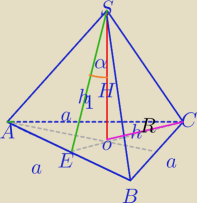Mila: V=72, R=2, |EC|=h

	|EO|
sinα=
	h1

1)

	2		2
R=		h, 2=		h ⇔h=3,
	3		3

|OE|=1

	a√3
h=		⇔2*h=a√3 /*√3
	2

2*3√3=a*3 a=2√3 2)

	1		1
V=		*		*a*h*H
	3		2

1		72
	*2√3*3*H=72⇔H=
6		√3

H=24√3 3) W ΔSOE: h₁²=|EO|²+H² h₁²=1+24²*3=1729 h₁=√1729

	1
4) sinα=
	√1729

Eta: Dokładnie , też mam taki wynik

Mila: To super