Ostrosłupy Esssssa: Dany jest ostrosłup prawidłowy trójkątny ABCS o podstawie ABC i wierzchołku S. Objętość tego ostrosłupa jest równa 72, a promień okręgu opisanego na podstawie ABC jest równy 2. Oblicz sinus kąta między wysokością tego ostrosłupa i jego ściana boczną. Przerysuj rysunek, zaznacz na nim kąt o którym mowa w zadaniu i wprowadź stosowane w rozwiązaniu oznaczenia.

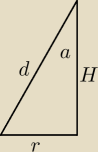
f123: R = 2

	2
R =		h (trojkata w podstawie)
	3

	2
2 =		h ⇒ h = 3
	3

	a√3
h =		⇒ a = 2√3
	2

	1		(2√3)2√3		√3
72 =		*		* H ⇒ H =		(ostroslupa)
	3		4		6

	1
r =		* h ⇒ r = 1
	3

Pitagoras d² = r² + H²

	7√3
Podstawiasz wartosci i wychodzi d =
	36

	r		6√39
a wiec sinα =		⇒ sinα =
	d		39

Esssssa: mi H wyszło 24√3

f123: a szedles moim tokiem rozumowania i moimi obliczeniami?

Esssssa: no tak.

	1		12√3
72 =		*		*H
	3		4

72 = U{3√3{3}} * H

	72
H =		= 24√3
	√3

f123: Masz racje, moj blad...

Esssssa:

3√3
	* H *
3

f123: i jak, wychodzi cos sensownego, zwiazanego z odpowiedza do tego zadania?

Esssssa:

	1
sinus wyszedł mi
	3

f123: no i elegancki sinus wyszedl

Esssssa: zrobiłem to w następujący sposób H = 24√3 a = 2√3

	1
(24√3)2+(		h)2=h2
	3

h=18√6

	b
sinα=
	c

	1   h 3
sinα=
	h

Mila: Masz odpowiedź do zadania ?, Coś mi mały kąt wychodzi. Może chodzi o promień okręgu wpisanego w podstawę?

Mila: 17:06 masz źle.

f123: @Mila jaki kat ci wychodzi? a raczej jego sinus?

Mila:

	1
sinα=		?
	√1729

f123: @Mila dokladnie