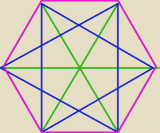
1 shanel: Punkty a, b, c, d, e, f są wierzchołkami sześciokąta foremnego. Rozpatrujemy zbiór wszystkich odcinków wyznaczonych przez te punkty. Z tego zbioru losujemy dwa odcinki. Jakie jest prawdopodobieństwo zdarzenia, że wylosowane odcinki mają taką samą długość? 0 pomysłu

Jerzy:

n(n − 3)
	= 9 ( przekatne) po 3 jednakowe)
2

6 − ilość boków

	3 1   6 2   3* *
P(A) =
	15 2

matmax: rysunek zrobiles?

Jerzy: Pomyłka: przekątne 9 ( 3 jednakowe i 6 jednakowych )

	3 1   6 2   3* *2*
P(A) =
	15 2

Jerzy: Jeszcze źle, ma być:

	3 2   6 2   *2*
P(A) =
	15 2

Jerzy: Oj, zmęczenie materiału:

	3 2   6 2   6 2   * *
P(A) =
	15 2

f123:

	6 2
@Jerzy skad drugie

Jerzy: Bo mamy 6 jednakowych przekątnych oraz 6 jednakowych boków.

Mila:

	3 1   6 2   6 2   + +
p=
	15 2