Bezwględna Chila: |x−2| + |x+4|=15

Jerzy: Rozwiązujesz w przedziałach: (−∞,−4) [−4,2) [2,∞)

Chila: tylko mam problem z odpowiedziami coś robię źle a nie wiem co

Jerzy: Pokaż obliczenia.

Chila: x ∊ (−4,∞) x=−¹⁷₂ x∊<4,2> brak x∊(2,∞) x=¹³₂ w odpowiedzi mam −7 i 3 zrobiłem sobie tabelke ze zamianami znaków i w x ∊ (−4,∞) zmieniam znak 2 razy w x∊<4,2> tylko w |x−2| a trzecim nawiasie nic nie ruszam

f123: skad wziales przedzial (−4, +inf)

Chila: no tam powinno być (−inf,−4) ale to dalej nie zmienia wyniku

Jerzy: Nie pokazuj wyniki, tylko jakie masz równania w tych przedziałach.

Chila: 1. −x+2−x−4=15 2. −x+2+x+4=15 3. x−2+x+4=15

Szkolniak: 1^o x∊D₁=(−∞;−4) ⇒ (|x−2|=−x+2 ∧ |x+4|=−x−4) −x+2−x−4=15

	17
−2x=17 ⇒ x=−		∊(−∞;−4)
	2

v2^o x∊D₂=<−4;2) ⇒ (|x−2|=−x+2 ∧ |x+4|=x+4) −x+2+x+4=15 6=15 ... brak rozwiązań v3^o x∊D₃=<2;+∞) ⇒ (|x−2|=x−2 ∧ |x+4|=x+4) x−2+x+4=15

	13
2x=13 ⇒ x=		∊<2;+∞)
	2

	17		13
suma 1,2 i 3 przypadku, zatem rozwiązaniami są liczby: −		i
	2		2

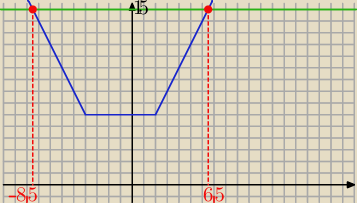
Eta: x∊(−∞, −4) | x∊<−4,2) | x∊<2,∞) =========================================== −x+2−x−4=15 | x−2−x−4=15 | x−2+x+4=15 x=−8,5 | sprzeczność | x= 6,5 ==== | | ==== Co też zgadza się z rysunku

Mila: |x−2| + |x+4|=15 L=|x−2|+|x+4|=|x−2|+|−x−4|≥|x−2−x−4|=6 6 najmniejsza wartość lewej strony dla x∊<−4,2> równanie nie ma rozwiązania w tym przedziale , bo 6≠15 1) x<−4 Równanie ma postać: −x+2−x−4=15 ....... 2) x>2 x−2+x+4=15 .......

Eta: A ja tak ładnie rozpisałam i jeszcze narysowałam

Mila: Bardzo ładnie

Chila: tak to prawda narysowane ładnie

Eta: