Geometria Nieogarnięty: W układzie współrzędnych zaznacz zbiór punktów, których współrzędne x, y spełniają nierówność: x²y>=xy². Dochodzę do czegoś takiego: xy(x−y)>=0 i nie bardzo wiem jak rozpisać przypadki

Bleee: Nierówność xy(x−y) ≥ 0 będzie spełniona gdy zajdzie jedna z sytuacji: 1) xy ≥ 0 oraz x−y ≥ 0 2) xy ≤ 0.oraz x−y ≤ 0 Rysujesz więc prosta f(x) = x (co masz z x−y = 0) I zaznaczasz odpowiednie obszary pamiętając że x*y ≥ 0 oznacza I i III cwiartke, natomiast x*y ≤ 0 oznacza II oraz IV cwiartke.

a7: x²y−xy²≥0 xy(x−y)≥0 x=0 lub y=0 lub x=y i sprawdzamy w wychodzących "podziałach" na podstawie podstawiania punktu z danego "sektora"

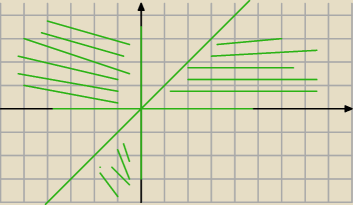
Szkolniak: Ja bym zrobił w ten sposób, że postępujemy według znaku iloczynu 'xy': 1) Dla x=0 ∧ y=0 nierówność ma postać 0≥0 − zdanie prawdziwe 2) Dla x<0 ∧ y<0 iloczyn ma znak dodatni, więc: y≤x 3) Dla x<0 ∧ y>0 iloczyn ma znak ujemny, więc: y≥x 4) Dla x>0 ∧ y>0 .. dodatni, więc: y≤x 5) Dla x>0 ∧ y<0 .. ujemny, więc y≥x I rysujesz odpowiednie przedziały i zaznaczasz

Nieogarnięty: Oki, dzieki