planimetria salamandra: Udowodnij, że w trójkącie prostokątnym suma przyprostokątnych równa jest sumie średnic okręgów opisanego na tym trójkącie i wpisanego w ten trójkąt.

	a+b−c
r=
	2

2r=a+b−c 2R=c a+b−c+c=a+b a+b=a+b może być? bo w książce mam troche inne rozwiązanie

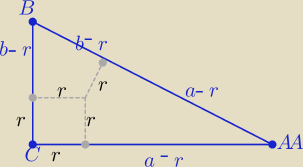
Eta: |AB|=2R⇒ a+b−2r=2R a+b=2R+2r i po ptokach

Eta: U Ciebie: 2r=a+b−c i c=2R 2r=a+b−2R a+b=2r+2R

salamandra: czyli mam ok czy nie w końcu

Eta: Nie bo napisałeś a+b= a+b i co z tego?

salamandra: Wiec równość się zgadza. a i b to przyprostokatne, Średnia okręgu opisanego=2R=c Wpisanego: a+b−c Wiec a+b=c+a+b−c a+b=a+b

Eta: Taki "koślawy " ten Twój dowód

Szkolniak: Też bym chyba to udowodnił jak salamandra Dopisałbym jeszcze ze L=P, cnw. i tyle

Eta: Dopisać należało jeszcze komentarz Po przekształceniach równoważnych ....L=P zatem a+b=2r+2R

Mila: Trzeba rozwiązać tak, jak podała Eta. I zapamiętać.

salamandra: Czyli podanie ogólnego wzoru nie przejdzie? Trzeba go udowodnić dodatkowo?

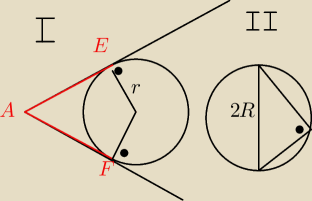
an: AE=EF Trzeba zrozumieć i zapamiętać na całe życie, jw jeżeli uważacie, że to potrzebne tylko na maturę, to jak skończą się restrykcje związane koronawirusem wyjdźcie na ulice i żądajcie usunięcia matematyki jako przedmiotu obowiązkowego ze szkół, po prostu szkoda waszego czasu i pieniędzy z naszych podatków.

salamandra: @an, ja rozumiem skąd to wynika, ale skoro istnieje już gotowy wzór na te promienie, to zadałem pytanie czy można po prostu się na nie powołać, niż je poniekąd jeszcze wyprowadzać w zadaniu.

Mila: salamandra, trzeba rozumieć problem, wzór to sprawa drugorzędna. Wszystkich wzorów nie zapamiętasz, a znając własności figur rozwiążesz zadanie.

salamandra: Wiem ale w tym przypadku wydawało mi się zasadne powołanie na te dwa wzory Co do tego co @an zrobił, to w 1−szym przypadku chyba AE=AF, a nie EF?

Mila: Tak, to pomyłka. |AE|=|AF| − punkty styczności okręgu wpisanego w kąt są jednakowo odległe od wierzchołka kąta.

an: >>chyba AE=AF, a nie EF<< nie chyba, a oczywiście