asymptoty Ola: Jak wygląda taka funkcja:

	4x3
y =
	x2 − 3x

wredulus_pospolitus: Tak wygląda: https://www.wolframalpha.com/input/?i=4x%5E3%2F%28x%5E2-3x%29

Jerzy: Bardzo ładnie wygląda.

janek191: Pewnie Ci chodzi o wykres tej funkcji?

Ola: W15:53 o i o to mi właśnie chodziło

Ola: można to bezkarnie podzielić przez x≠0

Ola: @janek wykres i asymptoty

Jerzy: Zacznij od dziedziny.

Ola: dziedzine juz mam teraz asymptoty czy musze liczyc ±∞

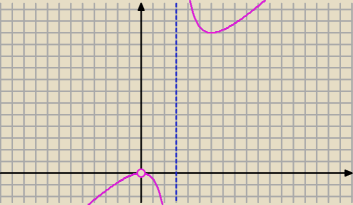
Ola: 0 nie należy a wolphram rysuje przez zero jest jedna pionowa x = 3 i ukośna

Mila:

	x2
limx→0		=0
	x−3

Mila: Zapomniałam 0 "4" przy x².

Ola: czyli jest taki "dziubek" tylko bez wierzchołka "0"

Mila: Tak.

Ola: a czemu nie liczy się granic z całej funkcji

	4x3
tzn. lim→0		= ∞
	x2 −3

Ola:

	4
sry to →		= 0
	∞

ale nie trzeba by zbadać z lewej i z prawej

Ola: tak przy x = 3

	4x3		108
lim→3−		=		→−∞
	x2−3x		0−

	4x3		108
lim→3+		=		→∞
	x2−3x		0+

Ola: proszę też o odp. na pyt. @ 16:17

Mila: W liczniku będziesz miała : 4*0=0 Skąd tam masz ∞ w mianowniku? Liczysz granicę po zał. x≠0 i po uproszczeniu. Wtedy nie ma potrzeby liczenia granic dwustronnych, bo nie masz w mianowniku zera.

Mila: Możesz policzyć granice w ±∞, ale nie ma poziomych asymptot, jest : pionowa x=3 i ukośna: y=4x+12

Ola: "Skąd tam masz ∞ w mianowniku?" bo podzieliłam licznik i mianownik przez x³ dz

Ola: to jak nazwać to "coś" w zerze nieciągłośc

Jerzy: Dla x = 0 ta funkcja nie istnieje.