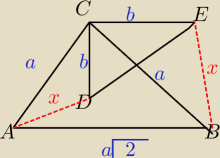
planimetria salamandra: Trójkąty prostokątne równoramienne ABC i CDE są położone tak jak na rysunku obok (w obu trójkątach kąt przy wierzchołku C jest prosty). Wykaż, że AD=BE jak zacząć?

f123: Bardzo proste, zobacz trojkaty ADC oraz CBE

salamandra: a, przystające i koniec

wredulus_pospolitus: salamandra −−− a w jaki sposób wykazałeś że są to trójkąty przystające Mam nadzieję, że nie było to tylko 'napisanie że są'

salamandra: A można nie wprost założyć, że teza jest prawdziwa i wtedy napisać, że te trójkąty są przystające na mocy cechy bbb, więc AD=BE?

wredulus_pospolitus: nie ... niewprost udowodnić możesz jedynie nieprawdziwość jakiegoś założenia / tezy

salamandra: to nie wiem jak to wykazać, myślałem, że dwa boki to wystarczający warunek dla przystawania, ale czytam, że jeszcze muszą mieć jakiś wspólny kąt, a tutaj go nie widzę

wredulus_pospolitus: Tak podejrzewałem przypatrz się na kąt: ∡ACE i zauważ, że jest on równy: ∡ACD + 90^o oraz 90^o + ∡BCE wniosek ...

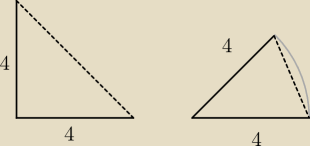
wredulus_pospolitus: masz przykład dwóch trójkątów z dwoma takimi samymi bokami

salamandra: aaa, ACD=BCE, teraz jasne

wredulus_pospolitus: I teraz ... mając dwa boki i kąt pomiędzy nimi równe dla obu tych trójkątów ... możesz powiedzieć, że są to trójkąty przystające