planimetria
salamandra:
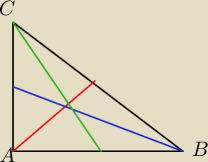
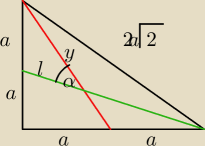
Oblicz tangens kąta ostrego utworzonego przez środkowe trójkąta prostokątnego równoramiennego
poprowadzone do przyprostokątnych
W grę wchodzi niebieska i zielona, czy czerwona i niebieska? Bo nie wiem to "poprowadzenie" czy
zaczyna się od wierzchołka, czy od boku.
Drugie pytanie− czy w przypadku trójkąta prostokątnego równoramiennego środkowa czerwona jest
równocześnie wysokością poprowadzoną z wierzchołka A?
25 mar 12:51
wredulus_pospolitus:
skoro środkowa ma być 'poprowadzone do przyprostokątnych' to z całą pewnością czerwona
odpada
25 mar 12:59
PW: Zasanie mówi o niebieskiej i zielonej środkowej. Środkowa jest definiowana jako prosta, więc
nie ma początku ani końca (nie "zaczyna się")..
25 mar 13:00
wredulus_pospolitus:
Drugie pytanie −−− tak ... będzie ona wysokością (i promieniem okręgu opisanego na tym
trójkącie)
25 mar 13:00
salamandra: no właśnie uświadomiłem sobie, że moje rozumowanie było bez sensu, bo jakby było, że
prowadzone do wierzchołka, to przecież z jednego wierzchołka (C) wychodzi zarówno
przeciwprostokątna i przyprostokątna,
dzięki
25 mar 13:01
a7:
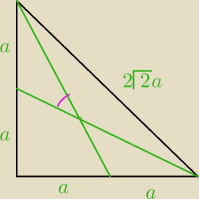
25 mar 13:01
25 mar 13:02
salamandra: nie zajrzę, robie sam na razie

25 mar 13:03
Eta:
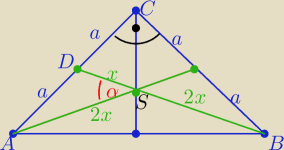
1/ wyznacz długość środkowej w zależności od "a"
i tw. cosinusów w ΔASD wyznacz cosα
i następnie sinα
tgα=...
i po ptokach

25 mar 13:18
salamandra:
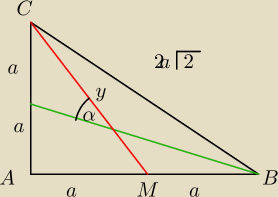
w Δ AMC
(2a)
2+a
2=x
2
5a
2=x
2
x=a
√5
jak to sfinalizować? tw. cos?
25 mar 13:21
salamandra: ok, spóźniłem się

25 mar 13:21
Eta:
x
2=5a
2 −−− tak zostaw
bo później łatwiej liczyć

| | x2+4x2−a2 | |
cosα= |
| =.......... |
| | 2*x*2x | |
25 mar 13:24
salamandra: nie mogę chyba tak zostawić, bo jak wtedy mam wyznaczyć "y"?
25 mar 13:43
salamandra:
x=a
√5
| | 5a2 | | 20a2 | | a√5 | | 2a√5 | |
a2= |
| + |
| −2* |
| * |
| *cosα |
| | 9 | | 9 | | 3 | | 3 | |
| | 3 | | 5 | | 15 | | 3 | |
tgα= |
| * |
| = |
| = |
| |
| | 5 | | 4 | | 20 | | 4 | |
25 mar 13:55
Eta:
Jest ok
krócej : z mojego rysunku
(3x)
2=5a
2
x
2=5a
2/9
| | 5x2−a2 | | 25a2−9a2 | |
cosα= |
| = |
| = 4/5 |
| | 4x2 | | 20a2 | |
sinα=3/5
tgα=3/4
25 mar 14:07
Eta:
Naucz się wreszcie wzoru
25 mar 14:08
salamandra: szczerze mówiąc, nie widzę tego Twojego przekształcenia "ot tak" do cosinusa

musiałbym
linijka po linijce zobaczyć, ale nie musisz, ważne, że rozwiązałem

25 mar 14:09
salamandra: a no tak, był taki wzór, coś z lekcji pamiętam nawet, ale nigdy go nie zastosowałem

25 mar 14:09
Eta:
Proste jak "budowa cepa"

a
2=b
2+c
2−2bc*cosα
2bc*cosα=b
2+c
2−a
2
25 mar 14:18
 Oblicz tangens kąta ostrego utworzonego przez środkowe trójkąta prostokątnego równoramiennego
poprowadzone do przyprostokątnych
W grę wchodzi niebieska i zielona, czy czerwona i niebieska? Bo nie wiem to "poprowadzenie" czy
zaczyna się od wierzchołka, czy od boku.
Drugie pytanie− czy w przypadku trójkąta prostokątnego równoramiennego środkowa czerwona jest
równocześnie wysokością poprowadzoną z wierzchołka A?
Oblicz tangens kąta ostrego utworzonego przez środkowe trójkąta prostokątnego równoramiennego
poprowadzone do przyprostokątnych
W grę wchodzi niebieska i zielona, czy czerwona i niebieska? Bo nie wiem to "poprowadzenie" czy
zaczyna się od wierzchołka, czy od boku.
Drugie pytanie− czy w przypadku trójkąta prostokątnego równoramiennego środkowa czerwona jest
równocześnie wysokością poprowadzoną z wierzchołka A?


 1/ wyznacz długość środkowej w zależności od "a"
i tw. cosinusów w ΔASD wyznacz cosα
i następnie sinα
tgα=...
i po ptokach
1/ wyznacz długość środkowej w zależności od "a"
i tw. cosinusów w ΔASD wyznacz cosα
i następnie sinα
tgα=...
i po ptokach 
 w Δ AMC
(2a)2+a2=x2
5a2=x2
x=a√5
w Δ AMC
(2a)2+a2=x2
5a2=x2
x=a√5


 x=a√5
x=a√5
 musiałbym
linijka po linijce zobaczyć, ale nie musisz, ważne, że rozwiązałem
musiałbym
linijka po linijce zobaczyć, ale nie musisz, ważne, że rozwiązałem 

 a2=b2+c2−2bc*cosα
2bc*cosα=b2+c2−a2
a2=b2+c2−2bc*cosα
2bc*cosα=b2+c2−a2
