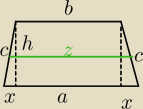
stereo jaros: Podstawa graniastoslupa prostego jest trapez rownoramienny, ktorego wysokosc jest rowna 5cm, a odcinek laczacy srodki ramion ma dlugosc 12cm. Wiedzac, ze przekroj tego graniastoslupa plaszczyzna zawierajaca krawedz boczna graniastoslupa i przekatna jego podstawy ma pole 130 cm², oblicz objętość tego graniastosłupa. Witam, przychodzi z takim problemem bo rozwiązuje to następująco.

	a + b
z = 12 =		=> a + b = 24 => 2c = 24 => c = 12 wyliczając bok x wychodzi mi √119 wie
	2

ktoś w czym jest błąd?

salamandra: skąd masz 2c=24?

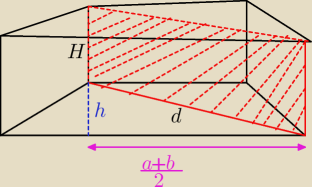salamandra: P=130 P=d*H P=d*5 130=d*5 d=26 chyba, że podana wysokość w zadaniu odnosi się do wysokości TRAPEZU, a nie graniastosłupa, to wtedy

a+b
	=12
2

h=5 5²+12²=d² pitagorejski, więc d=13 wtedy P=130 130=d*H ⇒ H=10

	a+b
Pp=		*H=6*10=60
	2

V=60*10=600

jaros: A no tak nie ma tak okręgu wpisanego w trapez kurde to jedyne co teraz wymyśliłem to żeby

	24
coś z potem pokąbinować P trapezu to 60 bo P=		* 5 a jaki krok dalej wykonać?
	2

jaros: Wytłumaczysz mi czym jest różowy odcinek?

salamandra:

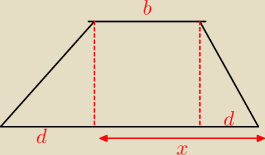
	a−b
d=
	2

	a−b		a+b
x=		+b=
	2		2

wredulus_pospolitus: Błędem było −−− tak jak Salamandra wskazał −−− założenie, że w ten trapez można wpisać na okrąg.

jaros: Dziękuje pięknie salamandra robiłeś już może podobne zadanie? bo to z tym x pierwszy raz wam widzę

salamandra: tak, ale z planimetrii, wtedy "poznałem" ten x.