Okrąg wpisany w trójkąt prostokątny
yellow_: Trójkąt prostokątny ABC jest prostokątny. Jeżeli z wierzchołka tego trójkąta wyprowadzimy
prostą prostopadłą do przeciwprostokątnej ,to ta prostopadła podzieli przeciwprostokątną na
odcinki o długościach 1cm i 4cm. Czy na podstawie tych danych można obliczyć promień okręgu
wpisanego w ten trójkąt,jeśli tak ile on wynosi?
25 mar 01:09
Jakiu: r=(2P)/(a+b+c)
wysokość na przeciwprostokątną dzieli trójkąt na 2 trójkąty prostokątne o bokach h,1,a i h,4,b
wiemy że a+b2=c2 a z powyższego otrzymamy a2=h2+12 i b2=h2+42
Podstawiając otrzymamy 2h2+17=25 −> h=2
Z tego wyliczamy a i b kolejno √5 i 2*√5
P=(1/2)*√5*2*√5=5
r=(2*5)/(√5+2*√5+5)=10/(3*√5+5)=
=(10(3√5−5)/20=(3√5−5)/2
Mam nadzieję że nie gafnąłem w obliczeniach
25 mar 01:26
a7:
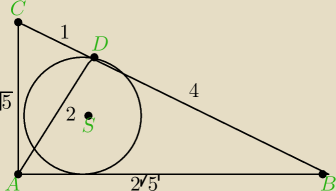
25 mar 01:27
Jakiu: Powinno tam być a2+b2=c2
25 mar 01:28
Eta:
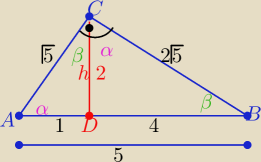
h
2=1*4 ⇒ h=2
a=2
√5, b=
√5 , c=5
25 mar 01:30

 h2=1*4 ⇒ h=2
a=2√5, b= √5 , c=5
h2=1*4 ⇒ h=2
a=2√5, b= √5 , c=5