Odległość prostej od innej prostej wolf: Znajdź równania prostych oddalonych od prostej x+2y−5=0 o odległość równą (pierwiastek z 5). Równania zapisz w postaci ax+by=c tak,by NWD(a,b)=1. Kompletnie nie wiem jak się zabrać za to zadanie. Mogę prosić o pomoc?

Szkolniak:

	1		5		1
2y=−x+5 → y1=−		x+		i druga prosta: y=−		x+b
	2		2		2

	5
z pierwszej prostej obieram punkt P=(0,		) i liczę jego odległość od prostej
	2

	1
y=−		x+b:
	2

	5   | −b|   2		5		5
		=√5 ⇔ |		−b|=		⇔ b∊{0,5}
	5   √   4		2		2

zatem szukane dwie proste mają równania: x+2y=0 oraz x+2y=10

Eta: @ Szkolniak bez obierania punktu k: Ax+By+C₁=0 p: Ax+By+C₂=0

	|C1−C2|
k∥p do d=
	√A2+B2

Szkolniak: Racja, zapomniałem o tym wzorze

a7:

	5
P=(0,		)
	2

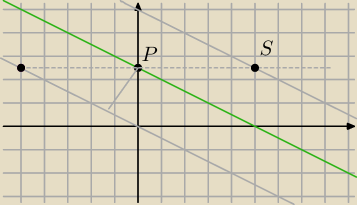
PS=2√5 wiadomo to gdyż mamy trójkąt ekierkę S=(2√5, −√5+b₁) (2√5)²+(−p{5+b−5/2)²=(2√5)² b₁=√5+5/2 czyli y=−1/2x+√5+5/2 czyli 2y+x−2√5+5=0 NWD(2,1)=1 (?) analogicznie druga prosta