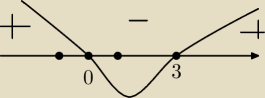
tryg kerdip: rozwiaz nierownosc cos²x−3cosx≤0 t=cosx ,t∊<−1,1> t²−3t≤0 t(t−3)≤0 i jak teraz było uwzgledniam tą dziedzinę zmiennej i będzie t∊<0;1>?

wredulus_pospolitus: t∊<−1,1>

kerdip: to jak rozwiązać tego typu nierowność?

a7: dobrze miałeś

a7: t∊<0,3> i t∊<−1,1> czyli t∊<0,1>

a7: ?

kerdip: no tak dałem i ,że cosx≥0 cosx≤1 przedziałami uwzględniłem i x∊<kπ;π+2kπ> i to będzie poprawnie?

a7:

	π		kπ
moim zdaniem to chyba x∊<−		+kπ,		+kπ> , ale nie jestem pewna, bo to nie jest
	2		2

moja mocna strona

Szkolniak: cos²x−3cosx≤0 niech t=cosx t²−3t≤0 t(t−3)≤0 t∊<0;3> ⇔ t≥0 ∧ t≤3 wracając z podstawieniem: cosx≥0 ∧ cosx≤3 (drugie spełnione dla x∊R) x∊<2kπ;π+2k>, k∊ℤ