prawdopodobienstwo Patryk: Cześć, Mam pytanie czy dobrze rozpisałem sobie prawdopodobieństwo za pomoca drzewka. Dane są dwie urny. Pierwsza zawiera 3 kule zielone i 4 czerwone, druga 4 zielone i 3 czerwone. Rzucamy raz sześcienną kostką do gry. Jeśli liczba oczek na kostce będzie mniejsza od 3 losujemy 3 kule z pierwszej urny, w przeciwnym wypadku losujemy 3 kule z drugiej urny. Oblicz prawdopod. 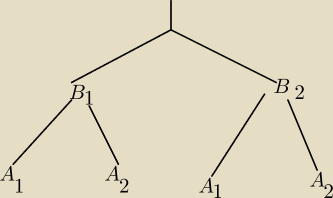tego, że spośród wylosowany kul będą 3 tego samego koloru Rozpiszę tylko lewą część drzewka − dla urny 1 bo chcę się tylko upewnić czy dobrze określiłem prawdopodobieństwa B1 = {1,2} B2={3,4,5,6} P(B1) = 1/3 // urna 1 P(B2) = 2/3 //urna 1

	3 3
P(A1|B1) =
	7 3

	4 3
P(A2|B1) =
	7 3

Jest dobrze?

wredulus_pospolitus: Czym jest A₁ i A₂

Patryk: A1 − trzy zielone kule A2 − trzy czerwone kule

adam:

wredulus_pospolitus: To co narysowałeś to nie jest pełne drzewko. Natomiast same prawdopodobieństwa są dobrze wyznaczone.

Patryk: O to mi chodziło. Ale rozrysowałem te zdarzenia których szukam i wychodziło by, że po lewej stronie drzewka i po prawej będę miał te same prawdopodobieństwa do wymnożenia?

wredulus_pospolitus: tak, będziesz miał to samo ... pamiętaj jednak że P(B₁) ≠ P(B₂) a czemu masz to samo. bo wyciągnięcie 3 kul tego samego koloru będzie takie samo gdy masz zestaw: 3 zielone i 4 czerwone co gdy masz 3 czerwone i 4 zielone i takie samo jakbyś miał 3 czarne i 4 różowe z niebieskimi słoniami

salamandra: A jednak Patryk walczysz z rachunkiem?

Patryk: A tak z ciekawości, jak powinno wyglądać tutaj "pełne" drzewko? Bo to drzewko, które narysowałem do rozwiązania zadania wystarcza?

wredulus_pospolitus: wystarcza do rozwiązania zadania ... jednak jeżeli w zadaniu trzeba było narysować pełne drzewo prawdopodobieństw, to nie ... nie wystarcza. Pełne drzewo winno posiadać wszystkie możliwe przypadki (czyli przypadki których później nie bierzesz pod uwagę, bo nie spełniają warunków zadania) ... czyli od zarąbania gałęzi.

Patryk: A dobra, rozumiem Dzięki za sprawdzenie i wyjaśnienie