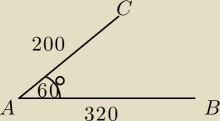
optymalizacja pytający: Trzy miejscowości A, B, C położone są tak jak na rysunku i połączone prostymi drogami. Z miejscowości C i A wyruszają jednocześnie samochody. Samochód z C jedzie do miejscowości A z prędkością 50 km/h. Samochód z A jedzie do miejscowości B z prędkością 80 km/h. Jaka będzie najmniejsza między nimi odległość w linii prostej? (odległość miedzy miastami jest w km (200km i 320km))

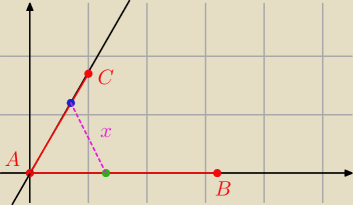
wredulus_pospolitus: A(0 , 0) B(320 , 0) C(x_o , x_o√3) |AC| = 200 −−−> 200 = √ x_o² + 3x_o² = 2x_o −−−> x_o = 100 Czyli C(100 ; 100√3) Oznaczmy: (AC)_t <−−− pozycja samochodu jadącego do miasta A w chwili t (AB)_t <−−− pozycja samochodu jadącego do miasta B w chwili t (AB)_t = ( 80*t , 0) (AC)_t = ( (100 − 50*sin60^o*t , 100√3 − 50*cos60^o*t) = ( 100 − 25t , √3(100 − 25t) ) D²(t) = ( 80t − (100 − 25t))² + 3(100 − 25t)² szukasz minimum tejże funkcji D²(t)

wredulus_pospolitus: można też inaczej do tego podejść −−− czyli z tw. cosinusów: X −−− punkt w którym jest samochód jadący do miasta A Y −−− punkt w którym jest samochód jadący do miasta B |XY|² = |AX|² + |AY|² − 2*|AX|*|AY|*cos60^o ⇔ |XY|²(t) = (200 − 50t)² + (320 − 80t)² − (200 − 50t)(320 − 80t) pochodna z tej funkcji i szukasz minimum