okrąg f123: Dany jest odcinek o końcach A = (a, 0) i B = (b, 0), gdzie a ≠ b. Uzasadnij, że zbiór punktów płaszczyzny P = (x, y) takich, że |AP| : |BP| = 1 : 3 tworzy okrąg

janek191: Jak się nie pomyliłem, to wychodzi takie równanie

	9a + b		3 a + 3 b
( x −		)2 + ( y − 0)2 = (		)2
	8		8

czyli równanie okręgu.

f123: no dobra ale jak do tego doszedles?

janek191:

I AP I		1
	=
I BP I		3

3 I AP I = I BP I 3 √(x −a)² = y² = √(x − b)² + y²

janek191: Itd.

Mila: To jest okrąg Apoloniusza.

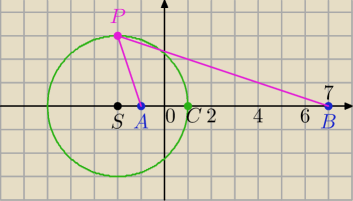
Mila: dla a=−1, b=7 3√(x+1)²+y²=√(x−7)²+y² (x+2)²+y²=9 |AP|=√10 |BP|=√3²+9²=3√10

AP		1
	=
BP		3

Ponadto:

AC		2		1
	=		=
CB		6		3

Eta: http://www.deltami.edu.pl/temat/matematyka/geometria/planimetria/2012/12/28/Okrag_Apoloniusza/