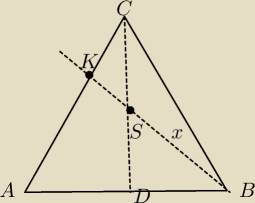
planimetria salamandra: Bok trójkąta równobocznego ABC ma długość a. Przez wierzchołek B i środek wysokości CD poprowadzono prostą która przecina bok AC w punkcie K. Oblicz |AK| jakaś podpowiedź? kombinowałem tylko w DSB żeby x wyznaczyć, ale to nic mi w zasadzie nie daje

Patryk: Spróbuj wyznaczyć BK a później z tw. cosinusów obliczysz AK: BK² = AB² + AK² −2*......*cos60

salamandra: Wtedy to już easy, ale jak do tego BK się dobrać właśnie

Patryk: W książce masz rozwiązanie do tego zadania

Jan: Jest to przecież rozwiązywanie trójkąta gdy dane są bok (AB) i kąty do niego przyległe (<BAC i <ABK − mamy tangens kąta ABK = (h/a)). Mam pisać dalej?

salamandra: No właśnie troche mi ono nie podchodzi, dlatego pytam

salamandra: Ile wynosi tg ABK?

Patryk: SD to polowa wysokosci ktora mozesz od razu policzyc, BD to polowa podstawy czyli a/2, z tego liczysz tg, literki a się skróca

Eta:

	2
|AK|=		a
	3

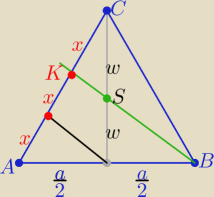
a7: BS=AS=a√74 z tw. Pitagorasa dlaΔDBS trójkąty ABK i EKS są podobne kkk ES/AB=KS/KB ES=a/2 KS=a√7/12 KB=a√7/3 cosα=(a/2):(a√7/4)=2√7/7 z tw. cosinusów KA²=KB²+AB²−2KB*ABcosα czyli |KA|=a/3*√16−6√3

a7:

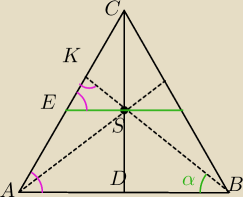
Jan: Poprowadź wysokość z wierzchołka A do boku BK, nazwijmy ją 'k'. Kąt w wierzchołku A to α, kąt ABK to β, a kąt przy wierzchołku K to γ = 180 − (α + β). Wtedy mamy: k/AB = sin(β) k = AB*sin(β) k/AK = sin(γ) czyli szukane AK = k/sin(γ) = AB*sin(β)/sin(γ) = AB*sin(β)/sin(α+β), ponieważ sin(γ) = sin(180 − (α+β)) = sin(α+β) Ostatecznie AK = a*sin(β)/sin(α+β) Oczywiście jest jeszcze problem jak wyliczyć te sinusy, ale wiemy że tan(β) = h/a = √3/2, to dalej to już tylko trygonometria i arytmetyka

wredulus_pospolitus: A ja to (wyznaczeni |BK|) zrobiłem z ciągu geometrycznego ... a konkretniej − nieskończonej sumy ciągu geometrycznego.

	3a2		7
|BS|2 = a2/4 +		= a2
	16		16

	√7
|BS| = a
	4

	√7   a   4		√7
|BK| =		=		a
	1   1 −   4		3

Wyznaczenie |AK| pozostawiam autorowi. Jak również zastanowienie się w jaki sposób tutaj 'wpierniczyłem' sumę nieskończonego ciągu geometrycznego. Jeżeli nikt nie wpadnie na to, to jutro zrobię rysunek i pokażę.

Eta: 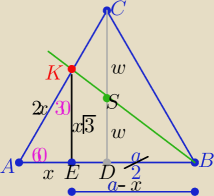2 sposób Z mojej ulubionej "ekierki" w=a√3/4 z podobieństwa trójkątów KEB i DSB

x√3		a−x
	=
a√3/4		a/2

	4x		2a−2x
		=
	a		a

6x=2a

	2
2x=|AK|=		a
	3

===============

Eta: I co tak milczycie?

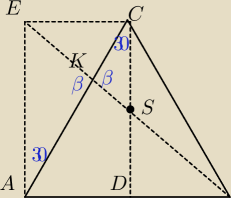
wredulus_pospolitus: Albo też można tak ΔCSK podobny do ΔAEK (podobieństwo KKK)

|CK|		|CS|		1
	=		=
|AK|		|AE|		2

	2
|CK| + |AK| = a −−−> |AK| =		a
	3

ale rozwiązanie Ety jest najpiękniejsze w swej prostocie.

Eta:

a7: I co ja robię tu ? Co ja tutaj robię 🙂

wredulus_pospolitus: Rano wejdzie Salamandra i się złapie za głowę na ile różnych sposobów można rozwiązać to zadanie

Eta:

wredulus_pospolitus: a7 −−− zrobiłeś byka przy podstawianiu do tw. cosinusów

	7		√7		2√7
|AK|2 =		a2 + a2 − 2*a2*		*
	9		3		7

	7		4		4
|AK|2 = a2(		+ 1 −		) = a2*
	9		3		9

a7: tak, tak, właśnie zauważyłam, dzięx

salamandra: No widzę ładnie temat odżył jak ja już się poddałem dzięki Wam wszystkim, teraz spróbuje przeanalizować, próbowałem rozgryźć ten ciąg geometryczny, ale nie potrafię. Ekierka− jak zwykle niezawodna, wniosek taki, ze muszę sobie dorysowywac jak najwiecej odcinków, kątów i wtedy może będę widział

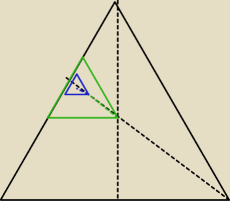
wredulus_pospolitus: co do ciągu geometrycznego 1) mamy wyjściowy trójkąt o boku a 2) tworzymy nowy trójkąt równoboczny o boku x, gdzie jego jeden wierzchołek jest połową wysokości poprzedniego

	1		1		1
Bok tego trójkąta to		*		a =		a
	2		2		4

Odcinek BK przecina połowę wysokości tego zielonego trójkąta. 3) tworzymy nowy trójkąt równoboczny, gdzie jeden z wierzchołków jest połową wysokości trójkąta.

	1		1		1		1		1
Bok tego trójkąta to		*		(		*		a) = (		)2a
	2		2		2		2		4

Odcinek BK przecina połowę wysokości tego niebieskiego trójkąta. itd.

	√7
b1 = |BS1| = a
	3

	1		√7		1
b2 = |S1S2| =		*|BS1| =		=		b1
	4		12		4

	1		1
b3 = |S2S3 =		*|S1S2| =		b2
	4		4

	b1
|BK| = ∑∞bi =
	1−q

a7: niezłe

Eta: Czytaj : wpis 01:11 i po ptokach

salamandra: Ok, czas się wziąć dziś do roboty− Eto− 01:11 to z podobieństwa jakoś, że te odcinki są równe x?

wredulus_pospolitus: 01:11 z podobieństwa trójkątów (podobieństwo: KKK) skala 1:4 (patrz podstawy trójkątów)

	1
stąd masz |KS| =		|BK|
	4

więc 3|KS| = |BS| −−−> |KS| = ... −−−−> |BK| = ...

wredulus_pospolitus: Natomiast Etusiowe jest z tw. Talesa. Poprowadziła po prostu równoległą do BK ze środka podstawy I mamy: Patrząc na proste AC i CD mamy:

|CK|		|KK2|
	=		<−−− z tw. Talesa
|CS|		|SD|

jako, że S jest w połowie wysokości to K jest w połowie CK₁ Później analogicznie patrzymy na proste AC i AB i analogiczna proporcja w celu wykazania, że |AK₁| = |KK₁| I stąd mamy: |AK₁| = |KK₁| = |KC|

salamandra: Nie wiem dlaczego KC również = x, tamte dwa trójkąty „widzę”

a7: https://matematykaszkolna.pl/strona/533.html

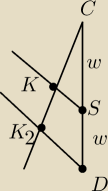
wredulus_pospolitus: z tw. Talesa mamy:

|CK|		|KK2|
	=		tak
|CS|		|SD|

wiemy, że:

	|CS|
|CS| = |SD| (czyli		= 1)
	|SD|

	|CK|
to jaka zależność będzie wyglądać
	|KK2|

salamandra: No ja znam to twierdzenie, bez przesady ale z wierzchołka C nie jest poprowadzona żadna równoległa prosta dlatego nie widzę tego KC

salamandra: Ok, już widzę, dzięki wredulusie

Eta: