Kąty
Michał : W trójkącie ostrokątnym ABC o kątach CAB=50 stopni, ABC=60 stopni, BCA=70 stopni
poprowadzono wysokości AQ, CR I BP. Wyznacz wymiary kątów trójkąta PQR
23 mar 20:34
wredulus_pospolitus:
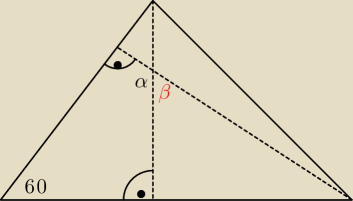
α = 360 − 90 − 90 − 60 = 120
β = 180 − α = 60
analogicznie pozostałe dwa kąty
23 mar 20:49
a7: tutaj trzeba wyznaczyć kąty trójkąta PQR a nie α i β
24 mar 13:15
wredulus_pospolitus:
Heh ... ja chciałem liczyć kąty dla trójkąta powstałego przez przecięcia tych wysokości
24 mar 13:21
a7: no dobra, ja nie umiem, a nikt tu nie błysnął jak na razie .........
24 mar 13:36
Michał : Witam, czy mógłby ktoś pomoc z resztą kątów?
24 mar 13:47
a7:
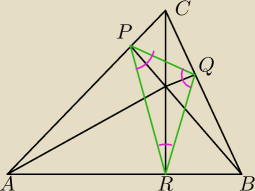
24 mar 14:09
Michał : Dzięki bardzo, a jak z miarami tych kątów?
24 mar 14:51
a7: no właśnie nie umiem i sama jestem ciekawa
24 mar 14:52
Michał : Siedziałem nad tym wczoraj trochę i też nie mam pojęcia
24 mar 14:54
a7: a są odpowiedzi jakieś?
24 mar 14:55
Michał : Nie ma właśnie
24 mar 14:55
f123: ciekawe zadanie, zrob na pewno lepszy rysunek i zauwaz, ze dostaniesz 3 deltoidy, a nastepnie
korzystasz z zaleznosci, ze mozesz na nich opisac okrag, pozniej dostajesz 3 trojkaty
rownoramienne ktore razem tworza trojkat PQR, powinienes otrzymac miary katow w trojkacie PQR
=> 55, 65, 60
24 mar 15:04
f123: Jednak nie, sory przeczytalem zle tresc zadania
24 mar 15:06
a7: z tymi deltoidami mi wyszło 80 60 40

zauważamy tam kąty wpisane oparte na tym samym łuku
24 mar 15:18
a7:
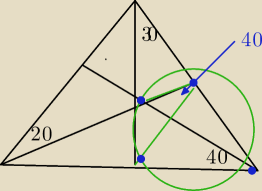
24 mar 15:21
a7: trochę trudno narysować, ale są kąty 40+40=80 30+30=60 20+20=40
24 mar 15:22
wredulus_pospolitus:
proszę o zdradzenie pewnej tajemnicy.
Skąd wiecie, że to jest deltoid

Na pierwszy 'rzut oka' na rysunek z 14:09 widzimy, że |BR| < |BQ|
24 mar 15:26
a7: to nie jest deltoid ale jest to czworokąt na którym można opisać okrąg, gdyż policzyłam kąty
24 mar 15:27
a7: także słuszna uwaga,ale rozwiązanie dobre tylko nie elegancko i nie precyzyjnie przedstawione
24 mar 15:27
wredulus_pospolitus:
Wybacz ... ale czym są wierzchołki tego czworokąta na którym można opisać okrąg i w jaki sposób
zostało sprawdzone że tak można uczynić

PS. Pamiętaj, że wysokości danego w zadaniu trójkąta NIE przecinają się w jednym punkcie

24 mar 15:31
24 mar 15:39
wredulus_pospolitus:
no popatrz ... zapomniałem o tym.
Okey ... no to czworokąt można wpisać wpisać w okrąg i jedziemy po kątach opartych na tym samym
łuku
24 mar 15:42
24 mar 15:42
Mila:
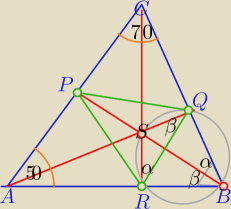
ΔPQR− trójkąt spodkowy, wysokości ΔABC są dwusiecznymi kątów wewnętrznych ΔPQR
W czworokącie RBQS sumy kątów przeciwległych mają po 180
o⇔
na tym czworokącie można opisać okrąg.
1)
|∡RBS|=90
o−50
o=40
o
|∡RQS|=|∡RBS| jako wpisane w okrąg oparte na łuku RS⇒
|∡Q|=80
o
2)
α=60−40
o=20
o⇒
|∡R|=40
o
3)
∡P=180−(80+40)=60
o
===============
24 mar 18:07
 α = 360 − 90 − 90 − 60 = 120
β = 180 − α = 60
analogicznie pozostałe dwa kąty
α = 360 − 90 − 90 − 60 = 120
β = 180 − α = 60
analogicznie pozostałe dwa kąty

 zauważamy tam kąty wpisane oparte na tym samym łuku
zauważamy tam kąty wpisane oparte na tym samym łuku

 Na pierwszy 'rzut oka' na rysunek z 14:09 widzimy, że |BR| < |BQ|
Na pierwszy 'rzut oka' na rysunek z 14:09 widzimy, że |BR| < |BQ|
 PS. Pamiętaj, że wysokości danego w zadaniu trójkąta NIE przecinają się w jednym punkcie
PS. Pamiętaj, że wysokości danego w zadaniu trójkąta NIE przecinają się w jednym punkcie 
 ΔPQR− trójkąt spodkowy, wysokości ΔABC są dwusiecznymi kątów wewnętrznych ΔPQR
W czworokącie RBQS sumy kątów przeciwległych mają po 180o⇔
na tym czworokącie można opisać okrąg.
1)
|∡RBS|=90o−50o=40o
|∡RQS|=|∡RBS| jako wpisane w okrąg oparte na łuku RS⇒
|∡Q|=80o
2)
α=60−40o=20o⇒
|∡R|=40o
3)
∡P=180−(80+40)=60o
===============
ΔPQR− trójkąt spodkowy, wysokości ΔABC są dwusiecznymi kątów wewnętrznych ΔPQR
W czworokącie RBQS sumy kątów przeciwległych mają po 180o⇔
na tym czworokącie można opisać okrąg.
1)
|∡RBS|=90o−50o=40o
|∡RQS|=|∡RBS| jako wpisane w okrąg oparte na łuku RS⇒
|∡Q|=80o
2)
α=60−40o=20o⇒
|∡R|=40o
3)
∡P=180−(80+40)=60o
===============