Trygonometria
Maja: Pole trójkąta ostrokątnego jest równe 780. Boki tego trójkąta mają długości |AB|=39 i |AC|=41 .
Oblicz. tg∡ ACB Błagam o pomoc głowie się nad tym od godziny
23 mar 20:31
Eta:
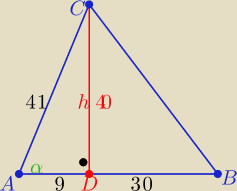
39*h=2*780 ⇒ h=40
|AD|=
√412−402= ...=9
tgα= .........
23 mar 20:42
ford:
1) Oznacz ∡CAB = α oraz ∡ACB = β
| | 1 | |
Ze wzoru na pole trójkąta |
| a*b*sinα dostajesz |
| | 2 | |
stąd
wyliczasz cosα z 1 trygonometrycznej
potem stosujesz tw. cosinusów i wyliczasz |BC|
wychodzi |BC| = 50
znając wszystkie 3 boki trójkąta myślę że sobie poradzisz
23 mar 20:44
a7:
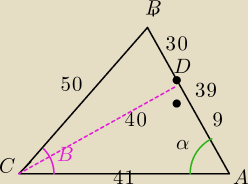
1/2*39*41sinα=780 ⇒sinα=40/41 ⇒|CD|=40 |AD|=9 |BD=30 |CB|=50
z tw. cosinusów 39
2=50
2+41
2−2*50*41cosβ ⇒cosβ=133/205 sinβ=156/205
_____________________
_____________________
23 mar 20:46
Eta:
Achhhhhhhh źle przeczytałam

|BC|=50,
tgγ= 156/133
23 mar 20:54
Eta:
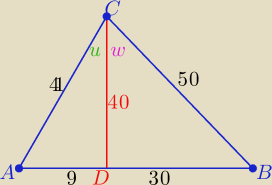
tgu= 9/40 , tgw=3/4
| | tgu+tgw | |
tg(u+w)= |
| = ......... = 156/133 |
| | 1−tgu*tgw | |
23 mar 20:57
Maja: Dzięki

23 mar 23:10
 39*h=2*780 ⇒ h=40
|AD|=√412−402= ...=9
tgα= .........
39*h=2*780 ⇒ h=40
|AD|=√412−402= ...=9
tgα= .........
 1/2*39*41sinα=780 ⇒sinα=40/41 ⇒|CD|=40 |AD|=9 |BD=30 |CB|=50
z tw. cosinusów 392=502+412−2*50*41cosβ ⇒cosβ=133/205 sinβ=156/205
1/2*39*41sinα=780 ⇒sinα=40/41 ⇒|CD|=40 |AD|=9 |BD=30 |CB|=50
z tw. cosinusów 392=502+412−2*50*41cosβ ⇒cosβ=133/205 sinβ=156/205
 |BC|=50,
tgγ= 156/133
|BC|=50,
tgγ= 156/133
 tgu= 9/40 , tgw=3/4
tgu= 9/40 , tgw=3/4
