Ostrosłupy
Marcinkiewicz: Wysokość ostrosłupa prawidłowego czworokątnego jest równa 24←←. Krawędź boczna jest nachylona
do płaszczyzny jego podstawy pod kątem, którego cosinus jest równy 5/13. Oblicz pole całkowite
tego ostrosłupa.
23 mar 20:03
Mila:
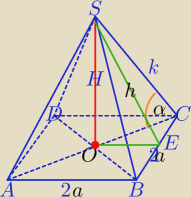
|AC|=2a
√2
| | 5 | |
cosα= |
| , α− kąt ostry |
| | 13 | |
| | 25 | | 12 | |
1) sin2α=1− |
| ⇔sinα= |
| |
| | 169 | | 13 | |
| | 12 | | 12 | | H | | 12 | | 24 | |
tgα= |
| ⇔ |
| = |
| ⇔ |
| = |
| |
| | 5 | | 5 | | |OC| | | 5 | | |OC| | |
|OC|=10
2) |AC|=20, 20=2a
√2⇔2a=10
√2
3) W SOE:
|OE|=5
√2
h
2=H
2+|OE|
2⇔h
2=24
2+(5
√2)
2
h=
√626
4)
| | 1 | | 1 | |
Pc= |
| *202+4* |
| *10√2*√626 |
| | 2 | | 2 | |
P
c= ... dokończ i sprawdź odpowiedź.
23 mar 20:49
Eta:
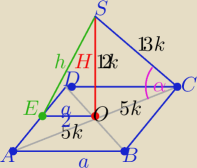
To może jeszcze tak:
cosα=5/13=5k/13k to H=12k
12k=H=24 ⇒ k=2 to |AC|=10k=20 a
√2=20 ⇒a=10
√2 ⇒ a/2=5
√2
w ΔEOS : h=
√242+(5√2)2
h=
√626
P
c=P
p+2ah =............
23 mar 21:40