Wyznacz styczne do okręgu przechodzące przez wspólny punkt A
bartman:
Wyznacz wszystkie równania stycznych "l" i "k"
dla okręgu "O" (x−6)2+(y−2)2=4,
które przechodzą przez wspólny punkt A=(−1,−3).
Narysuj układ współrzędnych oraz proste "l" i "k"
23 mar 19:44
wredulus_pospolitus:
Krok 1:
Wyznacz równanie ogólne prostej przechodzącej przez punkt A
Krok 2:
Sprawdź które z nich (dla którego 'a') mają dokładnie jeden punkt wspólny z okręgiem
Krok 3:
Wyznacz postać tychże prostych
23 mar 19:46
wredulus_pospolitus:
Inny sposób
Krok 1:
Wyznaczasz odległość pomiędzy punktem A i punktem O będącym środkiem okręgu.
Krok 2:
Wyznaczasz wzór okręgu o środku w punkcie A i promieniu spełniającym następujące równanie:
R2 + r2 = (|AO|)2
gdzie:
R −−− promień nowego okręgu
r −−− promień starego okręgu (r = 2)
Krok 3:
Wyznaczasz punkty przecięcia się tych okręgów. Są to punkty styczności prostej z okręgiem
Krok 4:
Wyznaczasz równanie prostej przechodzącej przez punkt A i jeden z wyznaczonych punktów.
Analogicznie dla drugiego wyznaczonego punktu.
23 mar 19:51
bartman: To wiem ale głupoty wychodzą
Dany jest okrąg o równaniu:
O: (x−a)
2+(y−b)
2=r
2
S=(a,b) − środek okręgu
r − promień okręgu
oraz prosta o równaniu
k: Ax+By+C=0.
d(S,k) jest to odległość punktu S od prostej k, czyli:
| | |A* a+B * b+C| | |
d(S,k)= |
| |
| | √A2+B2 | |
23 mar 19:58
bartman: Nie chodzi o metodę ale o wynik
23 mar 20:05
ford:
| | 7−2√2.8 | | 20 | | 2√2.8 | |
y = |
| x− |
| − |
| |
| | 9 | | 9 | | 9 | |
| | 7+2√2.8 | | 20 | | 2√2.8 | |
y = |
| x− |
| + |
| |
| | 9 | | 9 | | 9 | |
23 mar 20:14
bartman: skąd te 2√2.8 pod pierwiastkiem jeszcze gorzej niż mi 2√70
23 mar 20:41
ford:
bo to jest 2√14/5 a nie 2√14*5
23 mar 20:46
Mila:
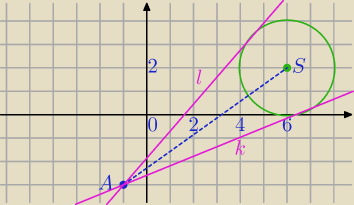
(x−6)
2+(y−2)
2=4, A=(−1,−3)
S=(6,2), r=2
y=ax+b
k:
ax−y+b=0
−a+3+b=0
b=a−3
k: ax−y+a−3=0
| | |a*6−2+a−3| | |
d(S,k)=2= |
| ⇔ |
| | √a2+1 | |
|7a−5|=2
√a2+1 /
2
| | 7+2√145 | | 7+2√145 | |
a= |
| lub a= |
| |
| | 9 | | 9 | |
Możesz tak zostawić, albo dalej przekształcać:
23 mar 21:54