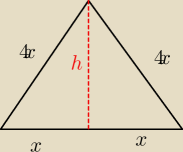
planimetria salamandra: Pole trójkąta równoramiennego jest równe 25. Oblicz długość promienia okregu wpisanego w ten trójkąt wiedząc, że ramię jest dwa razy dłuższe od podstawy. x²+h²=16x² h²=15x² h=x√15

	a*h		2x*x√15
P=		=
	2		2

25=x²*√15

	25		5√15
x2=		=
	√15		3

coś robię źle?

	a+b+c
chciałem wyliczyć bok, a później ze wzoru P=r*
	2

Patryk: Dobrze jest, po prostu taki głupi wynik wyjdzie

Patryk: Nie zawsze wynik wyjdzie piękny i ładny jak 2+2

wredulus_pospolitus: Pomijając to, że liczby są przeokropne to nic. No ale niestety takie liczby wyjdą

	5
r =
	x

salamandra:

	5
A skąd to r=		, rozszerzyłbys?
	x

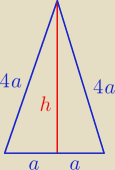
Eta: P²=a²*h² , h²=15a²

	5
to 15a4=625 ⇒ a=
	4√15

	P		5
r=		=
	5a		a

r=⁴√15 ========

wredulus_pospolitus: chociażby z:

	2P		2*25		5
r =		=		=
	a+b+c		10x		x

salamandra: aa

salamandra: Nie mogę tych wzorów zapamiętać nigdy, z tymi okręgami opisanymi/wpisanymi

wredulus_pospolitus:

	a+b+c
Toć chciałeś z tego wzoru korzystać (w końcu chciałem korzystać z P = r*		co jest
	2

przekształceniem tego co napisałem) ... więc jak mogłeś o nim nagle zapomnieć Coś mi tu kręcisz

salamandra: Tamten pamiętam (od dziś), ten nie zauważyłem, że powstaje przez przekształcenie haha

wredulus_pospolitus:

	5
ale jak widzisz 'kluczem do tego zadania' było umiejętne zapisanie x =
	4√15

co by nie było tragedii

Eta: Wniosek : zamiast pola P wprowadzić P² i po ptokach