Oblicz sinusa kąta między tymi stycznymi funkcji f Ania: f(x)=x²+1 y=−4x−1 y=4x−1 Proszę o pomoc

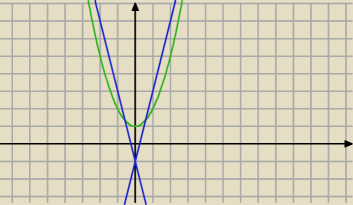
a7: to nie są styczne

Ania: proszę wybaczyć 2x rzecz jasna

Ania: 2x²

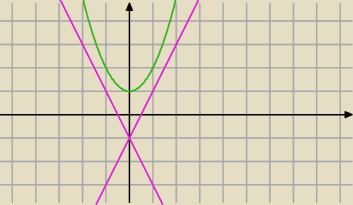
a7: to też nie są styczne

a7: aaa

Ania: f(x)=2x²+1

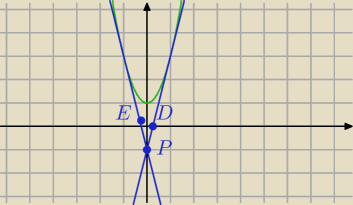
a7: P=(0,−1) D=(1/4,0) prosta ED y=−1/4x+b 0= −1/16+b ⇒b=1/16 y=−1/4x+1/16 E=(−17/60, 2/15)

	|ED|
teraz liczymy długości ED i EP i liczymy sinα=
	|EP|

a7: na pewno chodziło o sinus a nie o tangens?

PW: Szukamy ponktu wspólnego paraboli f(x) = 2x² + 1 i prostej y = 4x −1: 2x² + 1 = 4x −1 2x² − 4x + 2 = 0 x² − 2x + 1 = 0 (x − 1)² = 0 x = 1 Prosta i parabola mają dokładnie jeden punkt wspólny (1, 3). W punkcie o odciętej x₀ = 1 jest f'(x₀) = 4x₀ = 4•1 = 4 − rzeczywiście prosta y = 4x −1 jest styczna do paraboli w punkcie, (x₀, f(x₀)) = (1, 2•1² + 1) = (1, 3). Tego sprawdzenia można nie wykonywać (zakładamy, że treść zadania jest poprawna)

a7: @PW, ale czy sposób na policzenie sinusa jest ok czy można coś bardziej błyskotliwego?

PW: Mając punkt wspólny prostych i punkty styczności można zastosować wzór na sinus kąta między wektorami.