styczna jaros:

	1
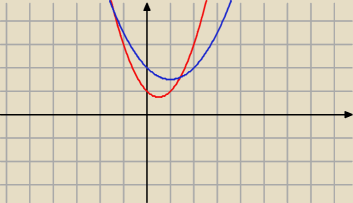
Wyznacz równania wspólnych stycznych do wykresów funkcji f(x) = x2 −x + 1 i g(x) =		x2
	2

−x +2 Jak się zaczyna coś takiego, najlepiej jakby mi ktoś wypisał kroki co i jak jak to werdulas ma w zwyczaju

wredulus_pospolitus: Krok 1: wzór ogólny stycznej f(x) (oznaczmy ja jako k(w)) Krok 2: wzór ogólny stycznej g(x) (oznaczmy ją jako m(q)) Krok 3: przyrównanie tych dwóch rodzin stycznych. Krok 4: sprawdzenie dla jakich w i q styczne mają te same współczynniki (a i b) Czyli otrzymasz układ dwóch równań z dwoma (w, q) niewiadomymi.

ford: Krok 1: y=ax+b − szukana styczna (trzeba wyliczyć a i b) Krok 2: Wykresy y=x²−x+1 oraz y=ax+b mają 1 punkt wspólny, więc układ równań { y=x²−x+1 { y=ax+b ma jedno rozwiązanie Równanie kwadratowe x²−x+1=ax+b wynikające z tego układu równań ma mieć 1 rozwiązanie (warunek Δ=0) Krok 3:

	1
To samo co w kroku 2 tylko dla wykresów y=		x2−x+2 oraz y=ax+b
	2

jaros: masz na myśli cos takiego? y + x² − x + 1 = 0 i to jako k(w)?

jaros: @ford Hmm ale dla 1 przyadku delte mam < 0 co wtedy?

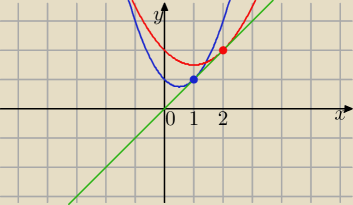
janek191: y = x

ford: ale nie.. nie chodzi mi o deltę z x²−x+1 chodzi mi o x²−x+1=ax+b porządkujesz to przerzucając na lewo x²−x−ax+1−b=0 x²−(1+a)x+1−b=0 i teraz wymagamy aby Δ=0 (1+a)²−4*1*(1−b)=0

wredulus_pospolitus: f(x) = x² − x + 1 f'(x) = 2x − 1 f'(w) = 2w − 1 styczna: y − f(w) = f'(w)(x − w) y − (w² − w + 1) = (2w−1)(x − w) y = (2w − 1)x − w² + 1 <−−−− to jest k(w) analogicznie drugą rodzinę stycznych i przyrównujesz: 2w − 1 = ... co to wyjdzie w drugiej rodzinie stycznych −w² + 1 = .... to co wyjdzie w drugiej rodzinie stycznych i otrzymamy w efekcie dla jakich konkretnie w i q mamy k(w) = m(q) (czyli 'identyczne' wzory stycznej)

jaros: I potem tak samo z drugą funckja i w układ równań to?

jaros: Tyczyło sie to jeszcze sposobu @ford

ford: tak dokładnie

jaros: @wredulus_pospolitus twój sposób jest w proponowany w odpowiedziach lecz go nie rozumiałem ale po twoim wyjacnieniu rozumiem

jaros: A mam pytanie ten wzór jaki zastosowałeś jest w kw? tzn karcie wzorów?

jaros: Bo mogę z niego korzystać bez wyprowadzania?

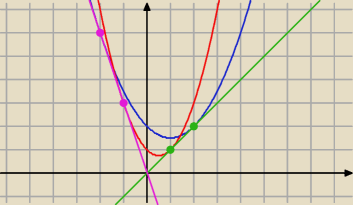
wredulus_pospolitus: g(x) = x²/2 − x + 2 g'(x) = x − 1 y = (q−1)(x−q) + (q²/2 − q + 2) y = (q−1)x − q²/2 + 2 więc mamy: 2w − 1 = q−1 −−−−> 2w = q −w² + 1 = −q²/2 + 2 −−−> −w² + 1 = −2w² + 2 −−−> w² = 1 −−−> −−− > w = 1 i q = 2 lub w = −1 i q = −2 a styczne to będą: 1) y = x 2) y = −3x

wredulus_pospolitus: ford −−− Twoja metoda jest niestety 'dziurawa', ponieważ: Dla w(x) = x³ + 2x− 7 istnieją takie styczne do tejże funkcji, które mają z tą funkcją więcej niż jeden punkt wspólny Gdybyśmy mieli funkcję z modułem, to już w ogóle by się 'posypało' (w punkcie w którym nie istnieje pochodna) bo byśmy mieli takie punkty dla których jest nieskończenie wiele 'stycznych'

ford: no jakby był wielomian 3−go stopnia albo inne cuda to wiadomo że moja metoda odpada Twoja jest bardziej uniwersalna

jaros: @wredulus_pospolitus mam jeszcze pytanie jak tam jest 2w − 1 = q−1 −−−−> 2w = q ====>>> to się bierze z porównania współczynniku a przy x −w2 + 1 = −q2/2 + 2 −−−> −w2 + 1 = −2w2 + 2 =======>>> porówanie współczynnika b ale tej linijki dalej nie rozumiem

jaros: czy po prostu zamieniłeś w 2 linijce q=2w a no tak racja debil ze mnie

wredulus_pospolitus:

	q2
−x2+1 = −		+ 2 <−−− porównanie współczynnika 'b'
	2

i teraz: podstawienie q = 2w −−− czyli q² = 4w² skracamy ... wyznaczamy dla jakiego 'w' zachodzi równość podstawiamy to (te) 'w' do ogólnego wzoru stycznej wyznaczonego wcześniej. dla sprawdzenia podstawiamy także 'q' do odpowiedniego wzoru stycznej i sprawdzamy czy wyjdzie dokładnie taki sam wzór (co dla odpowiadającemu mu 'w' ).

jaros: Dziękuje śliczne, wsm nigdy nie robilem takiego zadania to moje 1 gdzie porwónuje 2 styczne, zadanie za 6 pkt i znam universalną metodę, śweitnie

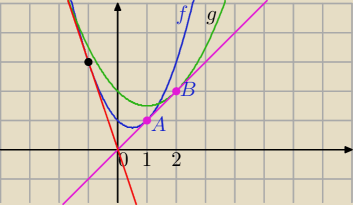
Mila: II sposób

	1
f(x) = x2 −x + 1 i g(x) =		x2−x+2
	2

Styczna : y=ax+b 1) f'(x)=2x−1 punkt styczności : A=(x₀,y₀) z wykresem f(x) g'(x)=x−1 Punkt styczności : B=(x₁,y₁) z wykresem g(x) A=(x₀, x₀²−x₀+1), B=(x₁, (1/2)x₁²−x₁+2) 2) styczna : y_(f)=(2x₀−1)*(x−x₀)+ x₀²−x₀+1=(2x₀−1)x−x₀²+1 y_(g)=(x₁−1)*(x−x₁)+(1/2)x₁²−x₁+2

	1
y(g)=(x1−1)*(x−x1)−		x12+2
	2

Porównanie wsp.

	1
2x0−1=x1−1 i −x02+1=−		x12+2⇔
	2

x₁=2x₀ x₀=1 lub x₀=−1 x₁=2 lub x₁=−2 4) równania stycznych : y=(2*1)x−1+1 y=x A=(1,1), B=(2,2) lub y=(2*(−1)−1)x−1+1 y=−3x A'=(−1,3 ) i B'=(−2,6) ==============

wredulus_pospolitus: co ja*