styczne jaros:

	1−6x2
Wyznacz równie stycznej do wykresu funkcji f(x) =
	6x2

	a1 − a2
a) tworzącej z osią OX kąt 120 tu ten wzór na tangens = I		I ?
	1 + a1a2

	1
b) przechodzącej przez punkt P(−3;		)
	2

Jerzy: Czy zapis funkcji jest poprawny ?

salamandra: a) co to za wzór? tg120=a wiec f’(x0)=a wiec

wredulus_pospolitus: (a) ale co to za wzór ... czym jest a₁ i a₂

Jerzy: a) NIE

wredulus_pospolitus: zauważ, dodatkowo, że:

	1−6x2		1
f(x) =		=		− 1
	6x2		6x2

jaros: a) wzór z karty wzorów z geo analitycznej, tak tak wyglada ta funkcja

jaros:

	1
jej pochodna to f'(x) = −
	3x3

jaros: Ktoś pomoże? przez tą pochodną wszystko mi się tak komplikuje i nie mam pomysłu na to zadanie

wredulus_pospolitus:

	1		1
f(x) =		− 1 =		*x−2 − 1
	6x2		6

z tej postaci licz pochodną

wredulus_pospolitus: jaros −−− poszukaj w internecie na przykład: "Analiza Matematyczna cz. I ćwiczenia" Gewert, Skoczylas I poćwicz liczenie pochodnych. Liczenie pochodnych powinno być 'automatyczne' i nie zajmować więcej niż 10 sekund (nie żartuję).

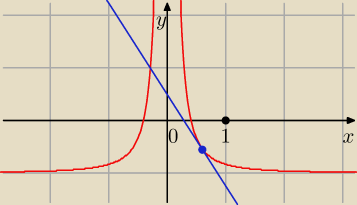
janek191: a) y = −√3 x + 0,5

jaros: Ok problem punktu b udało mi się rozwiązać zapis równań:

1
	= −3a + b
2

	1
a = f'(x0) −> −
	3x3

b = y₀ − f'(x₀)*x₀ Jakby kogoś chciał rozwiązać pkt b x₀ = 1 dla pomocy obliczeń

jaros: Janek a powiesz mi jak doszłaś do tej równania tej proste?

wredulus_pospolitus: (b) tak nie wyliczysz. Musisz wyznaczyć ogólną postać stycznej do tejże funkcji i sprawdzić dla jakiego x_o styczne te będą przechodzić przez punkt P dany w zadaniu.

jaros:

	1
ok równanie stycznej b) y = −		x −{1}{2}
	3

ktoś pomoże z a?

jaros: wyliczyłem

jaros: i wynik zgadza sie z odpowiedzią

wredulus_pospolitus: (a)

	1
f'(x) = −
	3x3

	1
f'(xo) = −		= −√3 (patrz jaki kąt ma być utworzony, a raczej wartość
	3(xo)3

tangensa tegoż kąta)

	1		1		1		√3
xo3 =		=		−> xo =		=
	3√3		(√33		√3		3

wstawiasz do wzoru na styczną

jaros:

	1
jak uprościć x3 =		?
	3√3

janek191:

	1		1
x =		bo x3 =
	√3		3√3

wredulus_pospolitus:

	1		1		1
xo3 =		= (		)3 ⇔ xo =
	(√3)3		√3		√3

jaros: ale jak pierwiastkujemy 3 stopniem to nie robi nam nie 5 stopnień?

wredulus_pospolitus: coooo

jaros: aaaa juz rozumiem dobrze, dziękuję pięknie

wredulus_pospolitus: a³ = 27 a³ = 3³ a = ... ile

jaros: w mojej głowie zrodził sie pomysł by pierwiastkować pierwiastek tzn. spierwiastkować P{27} ale to chyba nie tędy droga xd

jaros: a = 3

wredulus_pospolitus: a nawet jeśli byś tak szedł ... to ni hu hu nie miałbyś stopnia 5 tylko jak już to 6 (bo 2*3 = 6) natomiast ⁶√27 = 27^1/6 = (3³)^1/6 = 3^{3* 1/6} = 3^1/2 = √3