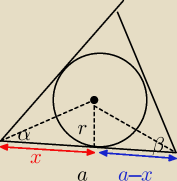
planimetria salamandra: Jeden z boków trójkąta ma długość a, zaś kąty trójkąta przyległe do tego boku mają miary α i β. a) wyznacz długość promienia okręgu opisanego na tym trójkącie b) wyznacz długości pozostałych boków trójkąta c) wyznacz długość promienia okręgu wpisanego w ten trójkąt

	a
a)		=2R
	sin(α+β)

	a
R=
	2sin(α+β)

mogę zostawić w takiej postaci nie rozwijając tego sin(α+β)? b) mam ok

	α		r
c)tg		=
	2		x

	r
x=
	α   tg   2

	β		r		r
tg		=		=
	2		a−x		r   a−   tgα2

	β		r		β		β   r*tg   2
r=tg		(a−		)=a*tg		−
	2		tgα2		2		α   tg   2

i jakim cudem w odpowiedzi nagle pozbywają się tego r po prawej stronie i jest

	α   β   a*tg *tg   2   2
r=		?
	α   β   tg +tg   2   2

Eta: α/2=w β/2=u

	r
r=(a−		)*tgw /*tgu
	tgu

rtgu=atgu*tgw−rtgw r(tgu+tgw)=atgu*tgw

	atgu*tgw
r=
	tgu+tgw

salamandra: Aż tyle kombinowania? Niezle, dzięki