Planimetria
Salazer:
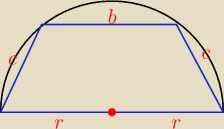
W półkole o promieniu długości 50 wpisano trapez o obwodzie długości 248 , którego wysokość
jest liczbą niewymierną, a dłuższa podstawa trapezu jest średnicą tego półkola.
Wyznacz długość ramienia tego trapezu.
Bardzo potrzebuje do 13 tego zadania
23 mar 12:00
a7:
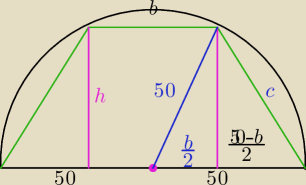
c=?
100+b+2c=248 ⇒ b=148−2c
50
2=(b/2)
2+h
2
50
2=(b/2)
2+(c
2−(25−b/2)
2)
mamy układ równań
podstawiamy b z pierwszego
c
2−50c+575=0
Δ=200
√Δ=10
√2
| | 50−10√2 | |
c1= |
| =25−5√2 c2=25+5√2 |
| | 2 | |
23 mar 12:35
a7: jeszcze trzeba sprawdzić czy wysokość jest niewymierna dla obu c,
poza tym mogłam się pomylić w obliczeniach.....
23 mar 12:37
Salazer: taam prawy bok powinien być (100−b)/2
23 mar 12:41
a7: no tak, no ale to podstaw prawidłowo i będzie prawidłowy wynik, ok?
23 mar 12:43
wredulus_pospolitus:
przepraszam ... ale gdzie masz ten układ równań, bo ja widzę tylko jedno równanie i jego
przekształcenie (postawienie za h2)
23 mar 12:44
a7: b=148−2c i to drugie
23 mar 12:48
wredulus_pospolitus:
a masz trzy niewiadome:
b , c , h
23 mar 12:51
wredulus_pospolitus:
oki ... dobra ... teraz ma to sens
23 mar 12:51
a7: dwie niewiadome c i b
c=40
23 mar 12:52
Norbert Gierczak: ez
23 mar 12:52
piotr skowyrski: ez
23 mar 12:52
Bogdan Siema: ez
23 mar 12:52
a7: ?
23 mar 12:53
a7: 2500=b2/4+c2−(50−b/2)2
z tego wychodzi
c2−5000+50(148−2c)=0
Δ=400
√Δ=20
c=40 lub c=60(to "za duże") c=40
23 mar 12:55
a7: c=60 jeszcze trzeba sprawdzić czy może mogłoby być
23 mar 12:57