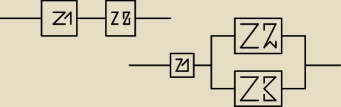
d FLOREK: Ż1, Ż2, Ż3, oznaczają żarówki, dla których dane są schematy fragmentów sieci elektrycznej. Prawdopodobieństwo nieprzepalenia się w czasie t godzin jest dla wszystkich żarówek jednakowe i wynosi 0,9. Zakładając, że żarówki przepalają się niezależnie od siebie wybrać wariant, dla którego prawdopodobieństwo ciągłego przepływu prądu przez dany fragment sieci jest większ.

ford: a) 0,9*0,9 = 0,81 b) 0,9*(1−0,1*0,1) = 0,9*0,99 = 0,891 (1−0,1*0,1) się wzięło stąd, że 0,1*0,1 oznacza prawdopodobieństwo, że przepalą się żarówki Z2 i Z3 1−0,1*0,1 jest zdarzeniem przeciwnym (przynajmniej jedna spośród Z2 i Z3 będzie świecić)

FLOREK: dziękuję bardzo za pomoc

wredulus_pospolitus: Szczerze mówiąc −−− bez liczenia można było się spodziewać że drugie rozwiązanie jest 'bezpieczniejsze' (ma mniejszą szansę aby zawieść). W pierwszym rozwiązaniu masz dwa elementy, którykolwiek z nich zawiedzie, cały układ pada. W drugim rozwiązaniu natomiast, jeżeli pierwszy element nie zawiedzie, to muszą aż dwa inne elementy zawieść, aby ten układ padł.