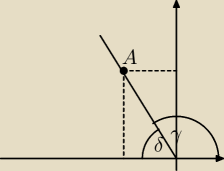
Jak to mam rozpisać, prosze o wytłumaczenie Paweł: Dla kątów: rozwartego γ oraz ostrego δ, widocznych na rysunku obok, prawdziwa jest równość Punkt A = (−2, 4) A) sinγ=cosδ B) sinγ=sinδ C) tg γ=tgδ D) cosγ=sinδ

a7:

	4		√2
sinδ=		=		⇒ δ=45o
	4√2		2

γ+δ=180 ⇒γ=180−δ ⇒ sinγ=sin(180^o−δ)= z wzorów redukcyjnych=sinδ czyli sinδ=sinγ B) trochę inaczej:

	4		√2
sinδ=		=		⇒ δ=45o
	4√2		2

	√2
δ=45o to γ=135o sinγ=(180o−45o)=sin45o=		=sinδ
	2

wzory redukcyjne https://matematykaszkolna.pl/strona/430.html

jc: r = odległość A od (0,0). sin δ = 4/r = sin γ cos δ = 2/r ≠ sin γ tg γ = 4/(−2)=−2, tg δ =4/2 = 2, tg γ ≠ tg δ cos γ = −2/r ≠ sin δ

a7: nawet nie trzeba wyznaczać sinδ, gdyż powiedzmy, że sinδ=x to sinγ=sin(180−δ)=sinδ= równe także x