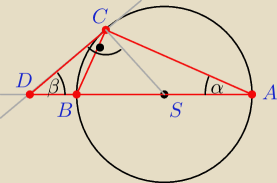
 Z punktu A leżącego na okręgu poprowadzono średnicę AB oraz cięciwę AC. Następnie przez punkt C
poprowadzono styczna do tego okręgu. Styczna ta przecina się z przedłużeniem średnicy AB w
punkcie D. Wiedząc, że promień okręgu ma długość 8 oraz że miara kąta α zawartego między
średnicą a cięciwą wynosi 30o, wyznacz pole trójkąta ACD.
|AS|=|SC|=8 i ΔASC − równoramienny o kącie 120o, stąd:
Z punktu A leżącego na okręgu poprowadzono średnicę AB oraz cięciwę AC. Następnie przez punkt C
poprowadzono styczna do tego okręgu. Styczna ta przecina się z przedłużeniem średnicy AB w
punkcie D. Wiedząc, że promień okręgu ma długość 8 oraz że miara kąta α zawartego między
średnicą a cięciwą wynosi 30o, wyznacz pole trójkąta ACD.
|AS|=|SC|=8 i ΔASC − równoramienny o kącie 120o, stąd:
| absinα | √3 | |||
PΔASC= | =32* | =16√3 | ||
| 2 | 2 |
| √3 | 8 | |||
tgβ= | i tgβ= | , stąd: y=8√3 | ||
| 3 | y |
| 8y | ||
PΔDSC= | =4y=32√3 | |
| 2 |


 Uwaga 2:
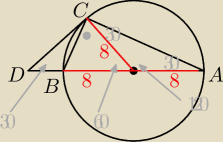
Można też (po wyznaczeniu β) zauważyć, że ΔACD jest równoramienny, |AC| = |CD|.
Co (przy informacji, że ΔSBC jest równoboczny) oznacza, że PBCD = PACS który już
wyliczyłeś.
Natomiast PBCS wyznaczysz bez problemu
Ale tak −−− w Twoim rozwiązaniu nie widać błędu
Uwaga 2:
Można też (po wyznaczeniu β) zauważyć, że ΔACD jest równoramienny, |AC| = |CD|.
Co (przy informacji, że ΔSBC jest równoboczny) oznacza, że PBCD = PACS który już
wyliczyłeś.
Natomiast PBCS wyznaczysz bez problemu
Ale tak −−− w Twoim rozwiązaniu nie widać błędu
| CS | ||
23:24 źle spojrzałam, nie było napisane tgβ= |  | |
| DC |

 i prawie koniec
i prawie koniec
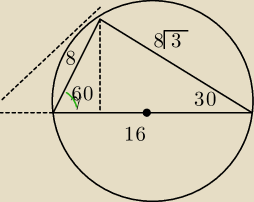
 |AD|=3*8=24 wysokość CE=4√3
|AD|=3*8=24 wysokość CE=4√3
| 1 | ||
P= | |AD|*|CE|= 48√3 | |
| 2 |