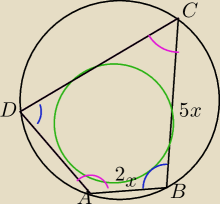
Optymalizacja jokeros2000: Rozpatrujemy wszystkie czworokąty ABCD , które są jednoczenie wpisane w okrąg i opisane na okręgu, w których |AB | = 2x , |BC | = 5x , i których obwód jest równy 10. Zapisz pole czworokąta ABCD jako funkcję zmiennej x . Wyznacz dziedzinę tej funkcji i oblicz długości boków tego z rozważanych czworokątów, którego pole jest największe.

jokeros2000: Wydaje mi się że trzeba to ruszyć z Herona

a7:

jokeros2000: Jak myślisz jak obliczyć te pozostałe boki?

a7: na razie tylko myślę

a7: mam coś tw cosinusów dla przekątnej dwa razy i może to jest trop

jokeros2000: Chodzi ci zapewne o przekątną AC?

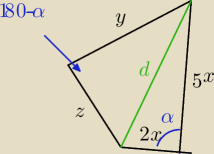
a7: 2x+y=5x+z ⇒ y=3x+z 2x+5x+y+z=10 ⇒ z=10−7x−3x−z ⇒ z=5−5x d²=4x²+25x²−20x²cosα d²=(5−2x)²+(5−5x)²−2(5−2x)(5−5x)cos(180−α)

jokeros2000: Nie wiem czy ta ostatnia linijka jest potrzebna. Wystarczy że boki uzależnie od x i później pójdę ze wzoru Herona na pole trójkąta, potem pójdzie już z górki z pochodną.

jokeros2000: Przepraszam nie Herona tylko Brahmagupty

jokeros2000: Na pole czworokąta

a7: o, nie znałam takiego wzoru, chyba da radę... trzeba spróbować

a7: POLE=√(5−2x)(5−5x)*5x*2x ?

jokeros2000: Dokładnie

a7:

	75√5		5
max =		dla x=
	32		8

https://www.wolframalpha.com/input/?i=sqrt%28%285%E2%88%922x%29%285%E2%88%925x%2910x%5E2%29+ boki 2x=1,25 3x= 3,125 z=1,875 y=3,75