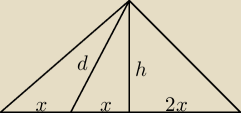
planimetria Patryk: Dany jest trójkąt równoramienny o podstawie długości 10 i kącie 120°. Oblicz: Długość odcinka poprowadzonego z wierzchołka kata rozwartego, który dzieli podstawę tego trójkąta w stosunku 1:4. Mi wyszło tak: d − szukana długość tg30 = h / 5

	5√3
h =
	3

x = 1/4 * 10 = 2,5 x² + h² = d² ..... d = 15 Będzie dobrze?

salamandra: Gdzie jest kat 120? Pytanie retoryczne ale wole się upewnić

salamandra: Aaa, ok, nie doczytałem

salamandra: Jeśli „D” to ten odcinek, to dzieli ci na odcinki x i 4x a nie x i 3x

wredulus_pospolitus: Nie ... nie jest dobrze.

	5√3		10√3		10		10
skoro h =		to ramię trójkąta = 2*h =		=		<		= 10
	3		3		√3		1

to jak niby d mogło Ci wyjść = 15 w końcu wiemy, ze h ≤ d ≤ ramię trójkąta

wredulus_pospolitus: proponuję: 1) wyznaczyć ramię trójkąta 2) wyznaczyć kąt przy podstawie 3) skorzystać z tw. cosinusów

Patryk: Mój błąd, faktycznie powinno być x i 4x