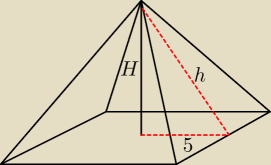
Proszę o szybką pomoc NiedzielnyMaturzysta: Pomocy! Rozważamy zbiór ostrosłupów spełniających następujące warunki: −podstawą ostrosłupa jest romb o boku 10 −wszystkie ściany boczne są nachylone do płaszczyzny podstawy pod tym samym kątem −suma długości wysokości ostrosłupa i wysokości jednej ściany bocznej jest równa 8 Wyznacz pole powierzchni całkowitej tego ostrosłupa, którego objętość jest największa.

salamandra: H+h=8 H=8−h 5²+(8−h)²=h² 25+64−16h+h²=h² 16h=89

	89
h=
	16

coś dziwnie wychodzi, więc nie będę robił dalej dopóki nikt nie potwierdzi

janek191: Tam nie ma 5

salamandra: To będzie promień okręgu wpisanego?

NiedzielnyMaturzysta: Wszystkie ściany boczne są nachylone do płaszczyzny podstawy pod tym samym kątem więc tak

NiedzielnyMaturzysta: Cały czas wychodzi mi zła pochodna (zła ponieważ miejsca zerowe są równe 0 albo ujemne)

salamandra: Pokaz obliczenia

NiedzielnyMaturzysta: Wyszło mi że h1−wysokość rombu ma sqrt(100−x²) czyli r (promień okręgu wpisanego w romb) ma połowe h1 z tw. Pitagorasa wyliczyłem H(wysokość ostrosłupa) i wyszła mi (356−x²)/64

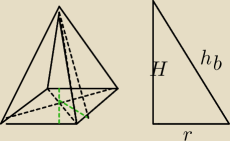
a7: V=1/3*10*h_p*H h_p=2r V=1/3*20r*H H+h_b=8 h_b=8−H z tw.Pitagorasa H²+r²=h_b² H²+r²=(8−H)² H²+r²=64−16H+H² r=√16(4−H)=4√4−H)

	1
V=		*20*4*√4−H*H
	3

teraz trzeba policzyć V'(H)

a7: ?

a7: https://www.wolframalpha.com/input/?i=y%3D%2880%2F3%29sqrt%284-x%29*x

	8
maksimum jest dla H=
	3

	1		8√3		16
Pc=Pp+Pb=10*ha+4*		*10*hb=20r+20hb=20*		+20*		=....
	2		3		3