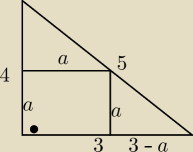
planimetria Patryk: Cześć, Mam kilka krótkich zadanek, ale nie mam do nich odpowiedzi więc chce się upewnic czy dobrze je robie: Dany jest trójkąt o przyprostokątnych 3 oraz 4. Oblicz długość boku kwadratu wpisanego w ten trójkąt, w taki sposób, że sąsiednie boki tego kwadratu leżą na przyprostokątnych tego trójkąta. Nie jestem pewien czy ten kwadrat będzie stykał się z przeciwprostokątną, ja zrobiłem to:

a		3−a
	=		// z podobieństwa
4		3

	12
a =		?
	7

Eta: ok ( dla podstawówki

Patryk: To tylko zadania powtórkowe

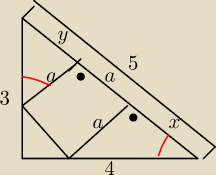
Patryk: Długość boku kwadratu wpisanego w ten trójkąt, w taki sposób, że jeden z boków tego kwadratu leży na przeciwprostokątnej tego trójkąta. czerwony kąt − α

	4
tgα =
	3

	4
y =		a
	3

	3
x =		a
	4

x+y+a = 5 16a + 9a + 12a = 60

	60
a =		?
	37

f123:

	12
Miales dobrze na poczatku, a =
	7

Patryk: Ale do pod spodem to już drugie zadanie

Eta: Dobrze a=60/37

Patryk: W tym samym trójkącie, oblicz: Długość boku możliwie największego trójkąta równobocznego wpisanego w ten trójkąt prostokątny, w taki sposób, że dolna podstawa trójkąta równobocznego leży na dłuższej przyprostokątnej trójkąta prostokątnego, a jeden z wierzchołków (trójkąta równobocznego) leży na przeciwprostokątnej(trójkąta prostokątnego) Jakaś wskazówka? Bo tutaj nie mam pomysłu na to...

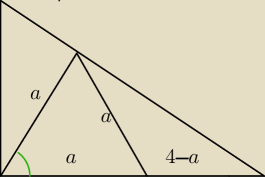
a7: PΔ=1/2*3*4=6 PΔ=1/23*asin30+1/2a²sin60+1/2(4−a)*asin120=6

	32√3−24
a=
	13

Patryk: Czyli największa długość tego trójkąta równobocznego będzie gdy jeden z jego wierzchołków będzie leżał gdzie wierzchołek kąta prostego tego dużego trójkąta?

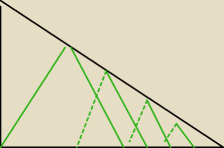
a7: moim zdaniem to logiczne na prawo już są tylko możliwe mniejsze a

a7: ponieważ przeciwprostokątna "idzie w dól" więc wysokość i bok trójkąta równobocznego maleje

Patryk: Rozumiem, dzięki