Matematyka Mk: W trójkącie ABC dane są wierzchołki: A = (0, –8), B = (–6, 0) oraz punkt C należący do osi Oy. a.) Wyznacz równanie prostej zawierającej dwusieczną kąta BAC. b.) Wyznacz współrzędne wierzchołka C tak, aby trójkąt ABC był prostokątny.

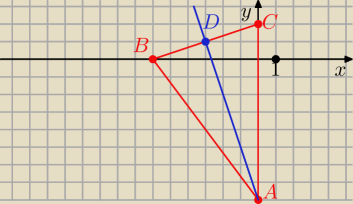
janek191: a) A = ( 0, −8) B = ( −6, 0) C =( 0,2) więc I AB I = I AC I D = ( − 3, 1) − środek BC Prosta AD jest dwusieczną kąta BAC.

janek191: b) 1) C = ( 0,0) 2) C = ( 0, y) → → BA musi być prostopadły do BC

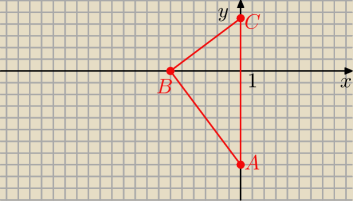
janek191: → BA = [ 6, − 8 ] → Bc = [ 6, y ] Mamy [ 6, − 8[ o [ 6 , y ] = 36 − 8y = 0 ⇔ 8y = 36 y = 4,5 C = ( 0; 4,5) ==========