optymalizacyjne xyz: Rozpatrujemy wszystkie trójkąty równoramienne o ramionach długości 6. Oblicz cosinus kąta między ramionami tego z tych trójkątów, dla którego objętość bryły powstałej w wyniku obrotu trójkąta dokoła prostej zawierającej jego podstawę jest największa możliwa. Oblicz tę największą objętość.

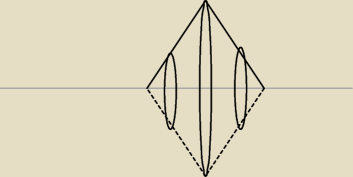
wredulus_pospolitus: otrzymujesz dwa stożki o promieniu podstawy = h_trójkąta i wysokości = 0.5*podstawa trójkąta

	1
Co się sprowadza do V =		π(htrójkąta)2* 'podstawa trójkąta'
	3

Wyraź jedną i drugą tych zmiennych za pomocą funkcji trygonometrycznych kąta α (lub α/2) i długości ramienia trójkąta (6)

xyz: mógłbyś to jakoś rozpisać? bo nie bardzo rozumiem