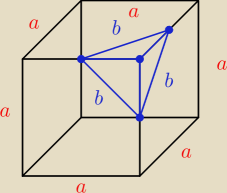
Sześcian, ostrosłup Szkolniak: W sześcianie o krawędzi długości a połączono środki krawędzi wychodzących z jednego wierzchołka i odcięto, tak powstały ostrosłup. Oblicz objętość powstałego ostrosłupa.

	a√2
'b' wyznaczam z twierdzenia Pitagorasa → b=
	2

domyślam się, że powstały ostrosłup jest ostrosłupem prawidłowym trójkątnym natomiast w jaki sposób mogę policzyć wysokość tego ostrosłupa?

wredulus_pospolitus: popatrz na ten ostrosłup z innej strony a raczej na ten graniastosłup ... zaraz Ci narysuję

salamandra: Wysokością nie będzie po prostu połowa krawędzi

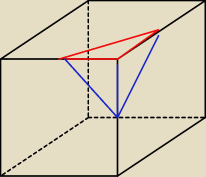
wredulus_pospolitus: Na ten ostrosłup popatrz tak jakby czerwony trójkąt był podstawą, wtedy P_p = A jego wysokość = ... Więc V = ...

wredulus_pospolitus: salamandra ... w momencie w którym Szkolniak wspomniał o ostrosłupie PRAWIDŁOWYM to oznacza, że za podstawę bierze pole przekroju (całkowicie niepotrzebnie)

Szkolniak: w takim razie:

	a2		a
Pp=		i H=
	8		2

	1		a2		a		a3
więc: V=		*		*		=		?
	3		8		2		48

wredulus_pospolitus: Da

Szkolniak: Super, dzięki

salamandra: Chyba nieważne który by wziął za podstawę to wysokością będzie połowa krawędzi? Czy się mylę?

wredulus_pospolitus: nie ... gdy weźmiesz za podstawę pole przekroju tego ostrosłupa (czyli w podstawie masz trójkąt

	a
równoboczny o boku a√2 ) to nie możesz mieć wysokości równej		bo by Ci inna objętość
	2

przecież wyszła

wredulus_pospolitus:

	a√2
tfu ...		−−− krawędź podstawy
	2

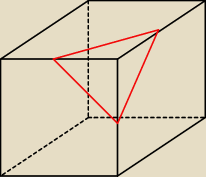
wredulus_pospolitus: szkolniak chciał to traktować jako podstawę

salamandra: To nawet wybiega poza moja wyobraźnie haha

Szkolniak: śmieszne jak szybko zmienia się zadanie jeśli spojrzysz na to tak jak pokazał to wredulus, a tak jak ja to chciałem rozpatrzeć

wredulus_pospolitus: A Ci powiem, że własnie to zadanie zdarzało się, że ludzie przychodzili tutaj na forum i właśnie chcieli w ten sposób liczyć objętość (i oczywiście mieli problem z wyznaczeniem wysokości ... co nie jest aż tak trudną sprawą). Zresztą, Ty nie czytałeś treści zadania, a treść to zapewne: Płaszczyzna przecina sześciościan w połowach trzech stykających się ze sobą krawędzi. Oblicz objętość odciętej części sześciościanu w stosunku do (np.) pozostałej jej części.

wredulus_pospolitus: Salamandra −−− i Ci powiem, że właśnie bardzo często ludzie czytając treść zadania podświadomie ustawiają pole przekroju jako podstawę (od tego wychodzą). Nie wiem ... pamiętasz jak kiedyś było zadanie z wyznaczeniem optymalnego kątu, czy tam długości krawędzi w ostrosłupie w którym tylko jedna krawędź (którą treść zadania sugerował jako krawędź podstawy) była zmienną, reszta była stała i równa 1. Też się wtedy męczyłeś nad tym zadaniem, ja Ci poradziłem byś sobie 'odwrócił' ten ostrosłup i nagle się okazywało, że P_p jest stałą i jedyną zmienną (wpływającą na objętość) jest wysokość i wszystko rozwiązałem 'rachu ciachu'

salamandra: Nie pamietam, ale w tym wypadku nie przyszłoby mi do głowy rozpatrywać tego tak jak Szkolniak, bo nawet tej jego „podświadomej” podstawy nie widziałem

wredulus_pospolitus: zanim zaczynałeś kombinatorykę −−− więc początek marca Jakoś tak

wredulus_pospolitus: Tak jak napisałem −−− nie widziałem, bo nie widziałeś treści zadania przed spojrzeniem na rysunek. Gdybyś najpierw przeczytał treść zadania, później zrobił rysunek, zaznaczył sobie najpierw punkty przecięcia się płaszczyzny, później zaznaczył przekrój tej płaszczyzny i dopiero na końcu samą figurę którą ten przekrój odcina ... wtedy z pewnością byś widział tenże przekrój