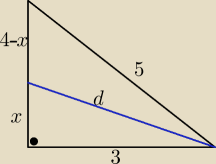
dwusieczna Patryk: Mam do policzenia dwusieczną trójkąta prostokątnego o bokach 3,4,5. Dwusieczna pada na bok o dł. 4. Czy mogę to zrobić w taki sposób? : tw. o dwusiecznej

x		4−x
	=
3		5

	3
x =
	2

z tw. pitagorasa: x² + 3² = d²

	3√5
d =		?
	2

Eta: tak

Patryk: Dzięki

salamandra: A co to za tw o dwusiecznej?

wredulus_pospolitus: https://matematykaszkolna.pl/strona/498.html

Eta: salamandra ... nie osłabiaj mnie

salamandra: No cóż, naprawdę nie miałem z tym styczności nigdy.

Saizou : salamandra to teraz za zadanie udowodnić to twierdzenie. Podpowiedź: twierdzenie sinusów się przyda

Szkolniak: Wesprę salamandrę i powiem ze ja również w swojej szkole nigdy nie miałem

Saizou :

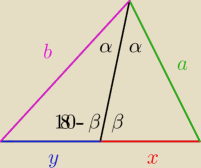
x		a		x		sinα
	=		→		=
sinα		sinβ		a		sinβ

y		b		y		sinα
	=		→		=
sinα		sin(180−β)		b		sinβ

zatem...

Eta: Nie mogę w to uwierzyć !

Eta: https://pl.wikipedia.org/wiki/Twierdzenie_o_dwusiecznej_k%C4%85ta_wewn%C4%99trznego_w_tr%C3%B3jk%C4%85cie

Szkolniak: Eta, z Tobą jako nauczycielką chyba żadne twierdzenie nie byłoby obce a tak to się trzeba posiłkować

Eta:

Saizou : To jeszcze zapoznajcie się z tw. Ptolemeusza

salamandra: Przerwa przedłużona do świat, to i na powtórkę planimetrii się znajdzie czas

Eta: