ciąg arytmetyczny
ratunku: Długości boków trójkąta prostokątnego tworzą ciąg arytmetyczny.
Najdłuższy bok ma długość 10 cm.
Oblicz długość promienia okręgu wpisanego w ten trójkąt.
20 mar 16:49
Eta:
Trójkąt ma boki długości : 6,8,10
20 mar 16:51
wredulus_pospolitus:
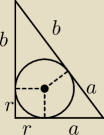
a+b = 10
2(r+b) = r+a + a+b
(r+a)
2 + (r+b)
2 = (a+b)
2
trzy równania ... trzy niewiadome ... liczysz
Wynik: boki mają długość 6,8,10 więc promień będzie równy r = 2
20 mar 16:53
ratunku: Czy mógłbyś pomóc mi obliczyć te długości boków? Nie wiem jak to zrobić z trzema
niewiadomymi...
20 mar 18:07
wredulus_pospolitus:
a+b = 10 −−−> b = 10 − a
r + b = 2a −−−> r = 3a − 10
więc mamy:
(r+a)2 + (r+b)2 = (a+b)2
(3a − 10 +a)2 + (2a)2 = (10)2
16a2 − 80a + 100 + 4a2 = 100
a2 − 4a = 0
a(a−4) = 0 −−−> a = 4 −−−> r = 2 koooniec
20 mar 18:15
ratunku: Dziękuję!
20 mar 18:57
 a+b = 10
2(r+b) = r+a + a+b
(r+a)2 + (r+b)2 = (a+b)2
trzy równania ... trzy niewiadome ... liczysz
Wynik: boki mają długość 6,8,10 więc promień będzie równy r = 2
a+b = 10
2(r+b) = r+a + a+b
(r+a)2 + (r+b)2 = (a+b)2
trzy równania ... trzy niewiadome ... liczysz
Wynik: boki mają długość 6,8,10 więc promień będzie równy r = 2