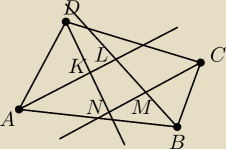
. Lewa: W czworokącie wypukłym ABCD poprowadzono dwusieczne kątów wewnętrznych. Ich przecięcia utworzyły czworokąt KLMN (rys. obok). Uzasadnij, że suma miar kątów ∡KLM i ∡MNK jest równa 1800. Bardzo proszę o rozwiązanie krok po kroku, bo nie wiem od czego zacząć

wredulus_pospolitus: Chyba miało być 180^o

Lewa: Tak, tak, przepraszam

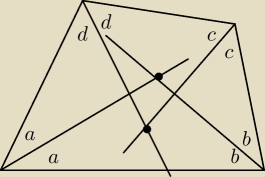
wredulus_pospolitus: Z sumy kątów w ΔABL wynika, że ∡ALB = 180 − (a + b) Z sumy kątów w ΔCDN wynika, że ∡CND = 180 − (c + d) czyli: ∡ALB + ∡CND = 360^o − (a + b + c + d) Natomiast z sumy kątów w tym czworokącie mamy: 360^o = 2a + 2b + 2c + 2d −−−−> a+b+c+d = ... Wniosek i c.n.w.

Eta: https://matematykaszkolna.pl/forum/388054.html

Lewa: Jejcia, trzeba to podzielić na 2 czy jak ?

Lewa: O dziękuję <3