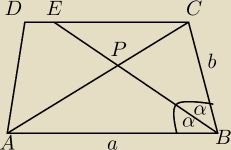
Oblicz część krótszej podstawy w trapezie Patryk: W trapezie ABCD dwusieczna kąta przy wierzchołku B, przecina przekątną AC w punkcie P, a krótszą podstawę CD w punkcie E. Wiedząc, że |AB| = 15, |BC| = 9 oraz pole trójkąta ABP jest równe polu powierzchni czworokąta APED, oblicz długość odcinka DE. Może ktoś dać jakieś wskazówki? Zauważyłem że kąt BEC = kąt EBC, co powinienem obliczyć aby móc obliczyć DE?

salamandra: Dawaj rysunek i spróbujemy

Patryk:

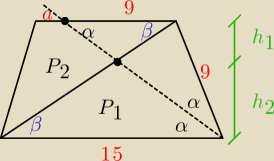
wredulus_pospolitus: ΔABP podobny do CEP

h2		15		5
	=		−> h2 =		h1
h1		9		3

P₁ = P₂

	15+a		15h2 − 15h1
15*h2 =		*(h1+h2) −−−> a =		−−−>
	2		h1 + h2

	25h1 − 15h1
−−−> a =		= ...
	8   h1 3

wredulus_pospolitus: A wcześniej jeszcze rozumowanie: Kąt α mamy przy E ze względu na tw. o kątach przy równoległych przeciętych jedną prostą. Z tego samego względu mamy odpowiednio kąt β zaznaczony przy C. Trójkąt BEC jest równoramienny ... stąd |EC| = 9

Patryk: Jasne, dzięki. Jeszcze prosiłbym o odpowiedź na jedno pytanie. Jak przeprowadzasz analizę takiego rysunku żeby dojść do rozwiązania? Czemu np. stwierdziłeś że będą potrzebne Ci wysokości? Zaczynasz raczej od końca( głównej niewiadomej) i patrzysz co możesz zrobić żeby do niej dojść, czy jakoś inaczej? Może trochę dziwne pytanie, ale mam nadzieję że wiesz o co mi chodzi i dasz radę coś powiedzieć na ten temat.

wredulus_pospolitus: Więc tak ... przy tym zadaniu (przyznam się otwarcie) byłem trochę jak ślepiec. 1) Nie wiedziałem jak to zrobić początkowo, więc ładowałem w rysunek WSZYSTKO (bez kąta β) co wiedziałem (łącznie z zaznaczeniem długości na które ta dwusieczna dzieli przekątną AC). 2) Napisałem równanie 2*P₂ = P₁ + P₂, z którego wyznaczyłem 'a' zależny od h₁ i h₂. 3) I zacząłem się zastanawiać jakie inne dwa równania mogę znaleźć, żeby utworzyć układ trzech równań z niewiadomymi (a, h₁, h₂) 4) Wtedy zauważyłem kwestię kąta β −−−> podobieństwo trójkątów −−−> proporcja h₁/h₂ −−−> wyznaczony a 5) Ścieram prawie wszystkie dane z rysunku (bo niewiadome na przekątnej wprowadziłem bardzo szybko) i podpisuję tylko to co istotne.

wredulus_pospolitus: PS. Jako, że w zadaniu była podana informacja o polu, to wiedziałem że MUSI być wykorzystany wzór na pole ... więc zaznaczenie wysokości to takie 'must have'

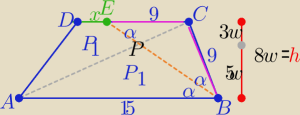
Eta: ΔBEC równoramienny to |EC|=BC|=9 Z podobieństwa Δ BCE i ΔABP w skali k=3/5 P(APBE)=2P(ABP)

x+15		1
	*8w= 2*		*15*5w ⇒x+15= 75/4
2		2

|DE|= x= 3,75 ==========

Eta: Poprawiam chochlika Z podobieństwa ΔPCE i ΔABP

Eta: Sorry I jeszcze jeden chochlik : P(ABED)=2P(ABP)