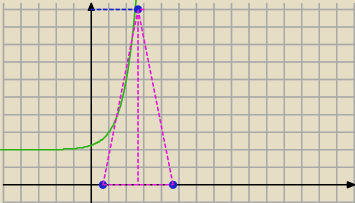
Funkcja wykładnicza + pole powierzchni trójkąta Pacio: Funkcja wykładnicza f określona jest wzorem f(x) = 4^x , dla każdego z ∊ R. Na wykresie funkcji g zdefiniowanej następująco: g(x) = f (x−1) + 2, gdzie x ∊ R, wyznacz taki punkt C, aby trójkąt o wierzchołkach A = (log₂ √2, 0) B = (1/2 log₂ 512, 0) I C miał pole powierzchni równe 20.

a7: log₂√2=1/2 1/2log₂512=9/2

	1		9
A=(		,0) B=(		,0) |AB|=4 czyli wysokość musi być 10 (bo Pole =20=1/2*4*10)
	2		2

czyli y=10 g(x)=10 g(x)=4^x−1+2 10=4^x−1+2 8=4^x−1 2³=2^2x−2 2x−2=3

	5
x=		y=10
	2

	5
C=(		,10)
	2