Graniastosłupy Tomek: W graniastosłupie trójkatnym prawidłowym ABCA'B'C' punkt P należy do krawędzi CC' . Pole powierzchni przekroju płaszczyzną ABP jest równe 540√3 . Oblicz pole powierzchni podstawy tego graniastosłupa. |AB|=24√3 |CP| : |PC'|=1/3

Tomek: :(

Eta: W treści pewnie jest : Oblicz pole powierzchni albo całkowitej albo bocznej bo dla pola podstawy , to nie ma co liczyć

	a2√3
Pp=		, gdzie a=|AB|=24√3
	4

P_p=.......

Szkolniak:

	ah
PΔABP=		=12√3*h
	2

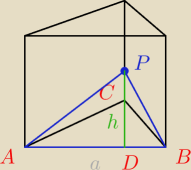
P_ΔABP=540√3, zatem → h=45 |CP|=x z ΔDCP:

	a√3
x2+(		)2=h2
	2

x²=2025−729 ⇒ x=27

|CP|		1
	=		⇒ |PC'|=81, zatem wysokość graniastosłupa: |CP|+|PC'|=108 ... i dalej co
|PC'|		3

tam potrzebujesz

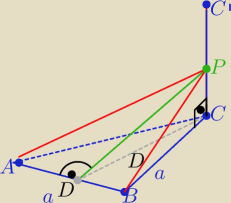
Eta: Dodam bardziej czytelny rysunek do obliczeń Szkolniaka

Tomek: jest o polu podstawy i objętości

Tomek: trzeba obliczyć pole podstawy* i objętość*

Eta: No to już wszystko masz podane jak na tacy ( wraz z rysunkami) i licz............