Nierówność
AHQ:
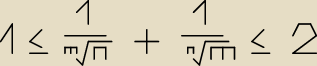
Niestety takich mądrych rzeczy nie idzie (chyba zapisać normalnie)

Oczywiście nierówność dla pewnych n,m∊N
19 mar 16:51
PW: "Dla pewnych m, n" − to znaczy pokazać taki przykład? O co pytasz?
19 mar 17:02
wredulus_pospolitus:
pod hasłem n,m ∊ N oczywiście rozumiemy także n ≠ 0 i m ≠ 0
1) niech m = const.
| | 1 | |
n1/m > 0 −−−−> |
| > 0 |
| | n1/m | |
| | 1 | | 1 | | 1 | | 1 | |
limn−>∞ |
| + |
| = [ |
| + |
| ] = 0 + 1 = 1 |
| | n1/m | | n√m | | ∞ | | 1 | |
2) niech m = n
| 1 | | 1 | | 2 | | 2 | |
| + |
| = |
| ≤ |
| = 2 |
| m1/n | | n1/m | | m1/n | | 1 | |
Wniosek i po sprawie
19 mar 17:16
AHQ: A zwykłymi nierównościami pomiędzy średnimi dałoby się zrobić ?
19 mar 18:33
AHQ: .? Bo raczej o to chodziło
21 mar 10:17
Saizou :
Da się
n=n*1*1...*1. (m−1 jedynek)
m=m*1*1...*1 (n−1 jedynek)
Am ≥ Gm
| | 1 | |
Nakładamy obustronnie funkcję f(x)= |
| |
| | x | |
(zmieniamy znak nierówności, bo funkcja f jest malejąca dla x>0)
===========+
| n+m | | 1 | | 1 | |
| ≤ |
| + |
| |
| n+m−1 | | n1/m | | m1/m | |
Ułamek po lewej stronie zmniejszymy, gdy zwiększymy mianownik
Czyli mamy oszacowanie z dołu.
21 mar 11:09
AHQ: @Saizou Mógłbyś wytłumaczyć co się dzieje w pierwszej części zadania ?
To znaczy jeszcze przed nałożeniem funkcji, bo same dalsze przekształcenia rozumiem
21 mar 21:24
Szkolniak: | | 1 | | 1 | |
1≤ |
| + |
| ≤2 − pewnie że idzie zapisać  |
| | n1m | | m1n | |
21 mar 22:29
Saizou :
Zapisuje n jako iloczyn n i m−1 jedynek, aby łącznie mieć ich m, czyli
n=n•1•1...•1
i stosuję nierówność między Am ≥ Gm (średnia geometryczna wprowadzi pierwiastek m−tego st.)
21 mar 23:23
AHQ: Ok, już jasne. Domyślam się, że oszacowanie z góry należałoby zrobić poprzez zastosowanie
Gm ≥ Hm ?
22 mar 10:51
AHQ: Oj, jednak się pomyliłem

Gm ≥ Hm
Dodając stronami, obracając i zmieniając znak mamy:
| 1 | | 1 | | 2+2nm−n−m | | 2−n−m | |
| + |
| ≤ |
| =2 + |
| ≤ 2 |
| n1m | | m1n | | nm | | nm | |
Chyba teraz się nie machnąłem ?

22 mar 13:22
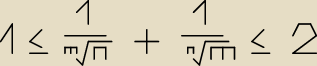 Niestety takich mądrych rzeczy nie idzie (chyba zapisać normalnie)
Niestety takich mądrych rzeczy nie idzie (chyba zapisać normalnie)  Oczywiście nierówność dla pewnych n,m∊N
Oczywiście nierówność dla pewnych n,m∊N

 Gm ≥ Hm
Gm ≥ Hm
