Wyznacz pole obszaru opisanego układem nierówności Frajvald: Witam mógłby ktoś pomóc z czymś takim? Wyznacz pole obszaru opisanego układem nierówności:

⎧	(x−3)2+(y−4)2<=6
⎜	x−y+5>=0
⎨	x+y−3>=0
⎩	x+y−11<=0

Próbowałem wyliczyć punkty przecięcia okręgu i prostych ale wychodzi mi że okrąg i proste nigdy się nie przecinają więc nie wiem jak to dalej ruszyć.

ite: Tu nie ma okręgu, jest koło. Pozostałe nierówności wyznaczają półpłaszczyzny.

Frajvald: Nie do końca rozumiem, mógłbyś pokazać jak zacząć to liczyć?

xyz: x−y+5 ≥ 0 −−> y ≤x + 5 (rysujesz prosta y=x+5 i zaznaczasz obszar ponizej tej prostej) x+y−3 ≥ 0 −−> y ≥ −x+3 (rysujesz prosta y= −x+3 i zaznaczasz obszar powyzej tej prostej) trzeci analogicznie natomiast (x−3)² + (y−4)² ≤ 6 to jest kolo (bo jest ≤ 6 a nie = 6, wtedy bylby okrag) zatem S(3,4) r = √6 (zamalowujesz te kolo w srodku)

ite: równanie okręgu (x−3)²+(y−4)²=6 równanie koła (x−3)²+(y−4)²≤6 równanie opisujące wnętrze koła (x−3)²+(y−4)²<6 równanie opisujące zewnętrze koła (x−3)²+(y−4)²>6 równanie prostej x+y−3=0 równania opisujące półpłaszczyznę x+y−3>0 lub x+y−3<0 bez brzegu /czyli bez prostej/ równania opisujące półpłaszczyznę x+y−3≥0 lub x+y−3≤0 z brzegiem /czyli bez prostej/ ↑ Czy to wiesz i umiesz to narysować? ↑

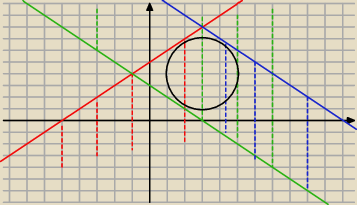
Jerzy: Wyglada na to,ze jest to pole tego koła.

Frajvald: ite tak umiem i narysywałem to tak samo jak Jerzy tyle że odpowiedz jest P = 24+4PI więc myślałem ze cos zle narysowalem

ite: Ja też mam taki rysunek i wynik jak Jerzy.