Liczę na pomoc, pozdrawiam serdecznie Buła: Zadanie 1. Okrąg opisany na trójkącie ABC ma promień 12 cm a bok AB ma długość równa 12√3 cm. Wyznacz miarę kąta ACB. Zadanie 2. Boki trójkąta ABC maja długości : 8cm, 9 cm i 10 cm. Wyznacz miarę najmniejszego kąta w tym trójkącie. Zadanie 3. W trójkącie ABC dane są długości boków │AB│= 14 cm, │BC│= 18 cm, │AC│= 20 cm. Wyznacz długości środkowych AD i BE. Zadanie 4. W równoległoboku ABCD dane są długości boków │AB│=12 i │BC│=8 . Kąt ABC ma miarę 45°. Wyznacz długości przekątnych tego równoległoboku.

xyz: zad 4. 2 razy tw. cosinusow

Buła: coś więcej?

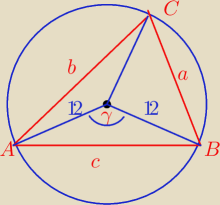
janek191: c = 12√3 Mamy (12√3)² = 144 + 144 −2*144*cosγ 432 − 288 = −288 cos γ 144 = −288 cos γ cos γ = − 0,5 γ = 120^o więc I ∡ ACB I = 0,5*120^o = 60^o

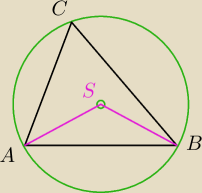
Tadeusz: W pierwszym ... policzysz kąt ASB a kąt ACB jest xrazy mniejszy

janek191: z.2 8² = 9² + 10² − 2*9*10*cos α 64 = 81 + 100 − 180 cos α 180 cos α = 117

	117		13
cos α =		=		= 0,65
	180		20

Odczytaj z tablic