Dla jakich wartości parametru m równanie sin^2x+sinx+m=0 ma rozwiązania? Marek Merkury: Dla jakich wartości parametru m równanie sin²x+sinx+m=0 ma rozwiązania? Zał: −1 ≤ sinx ≤ 1 sinx=t t²+t+m=0 Δ=1−4m, więc m ≤ ¹₄ Tyle udało mi się zrobić samemu i nie wiem co dalej. Czy nie powinienem jeszcze wcześniej założyć, że t≠0, ponieważ wtedy przestajemy mieć równanie kwadratowe, i tę opcję rozważyć osobno? Doszedłbym wtedy do tego, że gdy t=0, to i m=0, i tutaj znowu zastanawia mnie, co to właściwie znaczy, że m=0. Czy wtedy równanie ma nieskończenie wiele rozwiązań czy właśnie wcale nie ma rozwiązań? W rozwiązaniach z tyłu książki podają, że trzeba też wziąć pod uwagę g(1)≥0, dla g(t)=t²+t+m, ale nie wiem z czego to się wzięło.

wredulus_pospolitus: 1) zauważ, że wielomian ma ramiona skierowane do góry 2) tak więc, wielomian będzie miał co najmniej jedno rozwiązanie jeżeli zajdą następujące warunki: f(t) = t² + t + m a) Możliwość 1: I. f(1)*f(−1) < 0 wtedy masz dokładnie jedno rozwiązanie, b) Możliwość 2: I. f(1) > 0 II f(−1) > 0 III t_wierzchołka ∊ (−1 ; 1) wtedy masz dwa rozwiązania

wredulus_pospolitus: sorki ... słabe nierówności winny być przy wartościach , oraz t_wierzchołka ∊ <−1 ; 1>

Eta: Wielomian ma ramiona? Jak ja kocham takie sformułowania Dobrze,że teraz nie ma matury ustnej z matematyki ( bo bym padała ze śmiechu)

wredulus_pospolitus: ojjj ... ciiiii

Marek Merkury: Niestety nadal nie rozumiem zależności między tym, w którą stronę są skierowane ramiona paraboli, a tymi obliczeniami :c

wredulus_pospolitus: skoro ramiona paraboli są skierowane do góry ... to: 1) aby było jedno (ewentualnie dwa) rozwiązanie w przedziale <−1 ; 1> musi zajść jedna z sytuacji: a) f(−1) ≥ 0 i f(1) ≤ 0 lub b) f(−1) ≤ 0 i f(1) ≥ 0 bo w tym momencie mamy pewność, że istnieje taki a∊<−1 ; 1>, że f(a) = 0 a te warunki można zapisać krócej jako jeden: f(−1)*f(1) ≤ 0 (co gwarantuje nam że mamy 'niedodatnia' * 'nieujemna' )

wredulus_pospolitus: Czy tę część rozumiesz

Marek Merkury: Teraz tak

wredulus_pospolitus: A drugą sytuację rozumiesz

wredulus_pospolitus: Może jeszcze inaczej. Wyznaczyłeś kiedy Δ ≥ 0 .... czyli mamy tylko takie parabole które mają przynajmniej jeden punkt wspólny z osią OX.

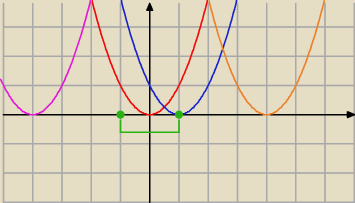
wredulus_pospolitus: Sytuacja 1: Δ = 0 chcemy, aby rozwiązanie było w przedziale <−1 ; 1> będzie wtedy gdy t_wierzchołka ∊ <−1 ; 1> zgoda

Marek Merkury: Zgoda

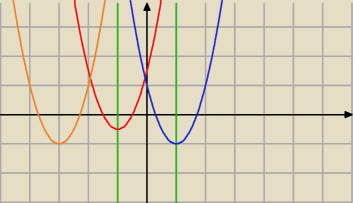
wredulus_pospolitus: Sytuacja 2: Δ > 0 i jedno (bądź dwa ... na krańcach przedziału) rozwiązanie w przedziale <−1 ; 1> Wtedy mamy to co opisałem powyżej ... iloczyn wartości funkcji na krańcach przedziału musi dać niedodatnią wartość

Marek Merkury: Teraz widzę

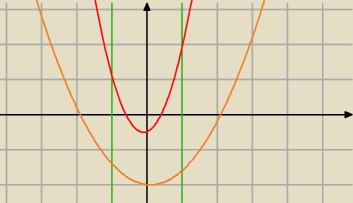
wredulus_pospolitus: A co jeżeli będą dokładnie dwa rozwiązania wewnątrz Wiemy, że jedno rozwiązanie będzie dla t < t_wierzchołka drugi dla t > t_wierzchołka, więc przede wszystkim musimy mieć t_wierzchołka ∊ <−1 ; 1> (tylko wtedy mogą być dwa rozwiązania wewnątrz tego przedziału). no ale to mało, bo jak rozróżnić te dwie parabole (a raczej ... odrzucić tą nie spełniającą warunków zadania) A no tym, żeby wartość funkcji na obu krańcach była nieujemna.

Marek Merkury: Omg, dzięki. Teraz wreszcie czaję co z czego wynika. Niech Ci Bóg wynagrodzi w (tu sobie sam wybierz) xD

Eta: W porzuceniu

wredulus_pospolitus: Nie moja droga ... już po fajeczce to było

wredulus_pospolitus: aaa ... jako nagroda ... ja tam wolę 50 dziewic

Eta: Takowe są jeszcze tylko na "innej planecie"

wredulus_pospolitus: uuuu dziewicowe kosmitki ... brzmi kusząco