twierdzenie Talesa maciek: 1. W trójkącie równoramiennym, w którym lACl=lBCl, punkt P dzieli wysokość CH, tak że lCPl / lPHl=3. W jakim stosunku prosta AP dzieli bok BC? 2. W trójkącie ABC na boku AB obrano punkt P, tak że lAPl / lPBl =5/6. W jakim stosunku odcinek CP dzieli środkową AS.

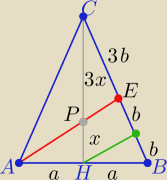
Eta: 1/ odp w stosunku 3:5

maciek: Super, dziękuje bardzo, ktoś ma pomysł na 2?

janek191: A nie 2 : 3 ?

Eta: Racja Janek ( źle odczytałam treść 3:2

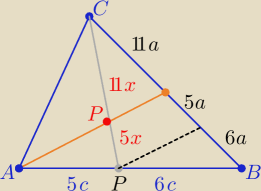
Eta: 2/ Podaj odp :........

maciek: Może ktoś pomóc i powiedzieć w jakim stosunku podzielona jest środkowa? Bo mam z tym problem

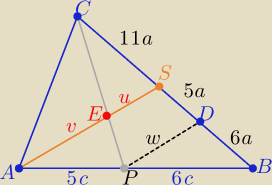
Eta: Myślałam,że dokończysz ? Szukany stosunek v/u

w		16		16
	=		⇒ w=		u
u		11		11

	v+u		11		11		8		5
i		=		⇒ v+u=		w =		u to v=		u
	w		6		6		3		3

	v		5
zatem		=
	u		3

Odcinek CP dzieli środkową AS w stosunku 5:3 licząc od wierzchołka A