Zadania z ostrosłupów
Żaneta: Witam, nie potrafię rozwiązać 2 zadań z matematyki. Prosiłabym o nie tylko rozwiązanie ale i o
wyjaśnienie. Z góry dziękuję
Zad.1. W ostrosłupie prawidłowym czworokątnym krawędź boczna o długości 6
√2cm jest nachylona
| | 2 | |
do podstawy pod takim kątem α którego cosα = |
| . Oblicz objętość tego ostrosłupa. |
| | 3 | |
Zad.2. Długość krawędzi podstawy ostrosłupa prawidłowego trójkątnego jest równa 2
√3, a kąt
nachylenia ściany bocznej do płaszczyzny podstawy ma miarę 60*. Oblicz objętość i pole
powierzchni całkowitej tego ostrosłupa.
Poziom 4 technikum.
18 mar 10:31
salamandra: 1. [...] do płaszczyzny podstawy czy krawędzi podstawy?
18 mar 10:34
Żaneta: W zadaniu jest do płaszczyzny podstawy
18 mar 10:35
salamandra:
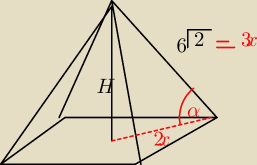
to musisz to napisac dokładnie, bo to są dwa różne kąty
6
√2=3x / : 3
2
√2=x
2x=4
√2
połowa przekątnej kwadratu=4
√2, więc cała przekątna 8
√2, więc krawędź podstawy 8.
Pp=64
3H=6
√10
H=2
√10
V=64*2
√10=128
√10
18 mar 10:41
Żaneta:
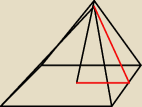
Rozumiem, dziękuję za rozwiązanie, mimo to w szkolę jestem pewna, że robiliśmy w ten sposób.
Mógł/Mogła byś mi wytłumaczyć, czy dałoby się rozwiązać to zadanie w ten sposób?
18 mar 10:47
salamandra: to jest kąt nachylenia ściany bocznej do płaszczyzny podstawy
18 mar 10:48
Żaneta: Dobrze, pomyliło mi się z drugim zadaniem, możemy kontynuować?

18 mar 10:50
salamandra: spróbuj sama, rysunek, zaznacz co się da.
| | 1 | |
Podpowiedź: odległość od spodka wysokości do krawędzi podstawy będzie równa |
| h (wysokości |
| | 3 | |
podstawy)
18 mar 10:53
Żaneta:
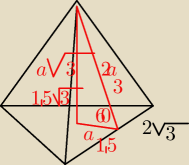
h= 3
2a= 3
a= 1,5
H=1,5
√3
Pb= 3
√3
Pc= 3
√3*4= 12
√3
V=
√3 * 1,5
√3= 4,5
Jeżeli gdzieś mam błąd to proszę mnie poprawić ♥
18 mar 11:26
salamandra: a=1
18 mar 11:29
Żaneta: Dlaczego 1?

18 mar 11:31
18 mar 11:31
Żaneta: W takim razie co z zależnością 30* 60* 90*?

?
18 mar 11:33
Jerzy:
| | 1 | |
Skoro h = 3 oraz a = |
| h , to a = 1 |
| | 3 | |
18 mar 11:34
salamandra: no skoro a=1, to teraz to "a" podstaw
18 mar 11:34
Żaneta: No oki ale skoro h = 2a to a nie będzie 1,5?
Jeżeli się mylę to podstawiam pod a=1 i rozwiązuje zadanie, tylko chciałabym to zrozumieć

18 mar 11:39
salamandra: no skoro a=1, to 2a=2 a nie 1,5, prawda?
18 mar 11:39
Żaneta: No dobrze ale na rysunku h tego trójkąta równobocznego jest równe 2a a skoro h ze wzoru na
wysokość trójkąta równobocznego równe jest 3 to nie znaczy, że 2a=3?
Mam mały mętlik w głowię, przepraszam za taką dużą ilość pewnie niepotrzebnych pytań
18 mar 11:43
salamandra: trójkątem równobocznym jest podstawa a nie ściana boczna!
18 mar 11:44
Jerzy:
Mieszasz pojęcia : wysokość podstawu bryły jest równa 3a , natomiast h to wysokość ściany
bocznej.
18 mar 11:46
Żaneta: Czyli całe zadanie do wyrzucenia

Nooo to jeszcze raz

18 mar 11:47
Jerzy:
h oblicz za pomocą funkcji trygonometrycznej.
18 mar 11:47
Jerzy:
Na razie jest OK. Policz wysokość ściany bocznej.
18 mar 11:48
salamandra: Oznaczyłas h jako wysokość podstawy i jako wysokość ściany bocznej, stad to zagmatwanie
18 mar 11:49
18 mar 11:49
Żaneta: Ale h=3 bo wzięliśmy wzór na wysokość trójkąta równobocznego ... Czyli już cała reszta się
sypie

18 mar 11:50
Jerzy:
| 1 | | 1 | |
| = |
| ⇔ h = 2 ( wysokość ściany bocznej ) |
| h | | 2 | |
18 mar 11:51
salamandra: jest wszystko ok, tykko to „a” źle wyliczylas
18 mar 11:51
Jerzy:
Nic się nie sypie. Wysokość podstawy jest równa 3a , wysokość ściany bocznej h = 2
i teraz licz dalej.
18 mar 11:52
Jerzy:
Oznacz bok podstawy jako x ( a wprowadza kolizję oznaczeń)
hp − wysokość podstawy i hp = 3
h − wysokość ściany bocznej i h = 2
18 mar 11:58
Żaneta: Czyli skoro hp = 3
a bok podstawy = 2
√3
| | 1 | |
to ze wzoru na pole trójkąta równoramiennego |
| *2√3*2=2√3 |
| | 2 | |
To możliwe, żeby bok podstawy był równy tyle samo co powierzchnia ściany bocznej?

18 mar 12:10
Żaneta: To zadanie mnie przerasta

18 mar 12:13
Jerzy:
A jeśli masz trójkąt o podstawie 5 i wysokości 2 , to jakie jest jego pole ?
18 mar 13:25
 to musisz to napisac dokładnie, bo to są dwa różne kąty
to musisz to napisac dokładnie, bo to są dwa różne kąty
 Rozumiem, dziękuję za rozwiązanie, mimo to w szkolę jestem pewna, że robiliśmy w ten sposób.
Mógł/Mogła byś mi wytłumaczyć, czy dałoby się rozwiązać to zadanie w ten sposób?
Rozumiem, dziękuję za rozwiązanie, mimo to w szkolę jestem pewna, że robiliśmy w ten sposób.
Mógł/Mogła byś mi wytłumaczyć, czy dałoby się rozwiązać to zadanie w ten sposób?

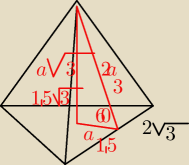

 ?
?

 Nooo to jeszcze raz
Nooo to jeszcze raz 


