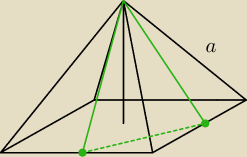
stereometria salamandra: Spośród wszystkich ostrosłupów prawidłowych czworokątnych o krawędzi bocznej długości a wybieramy ten, dla którego przekrój płaszczyzną przechodzącą przez środki dwóch sąsiednich krawędzi podstawy oraz wierzchołek ostrosłupa ma największe pole. Znajdź objętość tego ostrosłupa. jakaś podpowiedź? gdyby podana była krawędź podstawy a nie boczna, byłoby o wiele łatwiej

Saizou : Zauważ że zielone odcinki na ścianach bocznych to wysokości. Wprowdz 2x jako długość podstawy i próbuj dalej

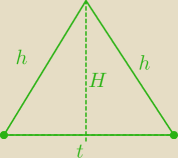salamandra: t=odcinek przerywany na rysunku h− wysokości ścian bocznych H− wysokość przekroju niech 2x− krawędź podstawy x²+x²=t² t=x√2 x²+h²=a² h²=a²−x²

	x√2
H2+(		)2=h2
	2

H²+x²=h² H²+x²=a²−x² H²+2x²=a² H²+t²=a² H²=a²−t²

	t*√a2−t2
P=		i szukać maksimum tego?
	2

Patryk: t chyba też musisz od a uzależnić ?

Saizou : Popraw ostatniego Pitagorasa

salamandra:

	√t2a2−t4
P=
	2

f(t)=−t⁴+t²a² f'(t)=−4t³+2a²t f'(t)=0 −4t³+2a²t=0 −2t(2t²−a²)=0 t=0 v 2t²=a²

	1
t2=		a2
	2

	√2		√2
t=		a v t=−		a
	2		2

	√2		√2
max dla t=		a, bo dla −		a nie należy do dziedziny, bo t>0
	2		2

salamandra: Gdzie dokładnie Saizou, bo nie widzę, tyle się narobiłem i coś źle przed?

Patryk: Ten ulamek z x−em zle podniosles to kwadratu

salamandra: o fak, mianownika nie podniosłem.....

salamandra:

	x√2
H2+(		)2=h2
	2

	1
H2+		x2=h2
	2

	1
H2+		x2=a2−x2
	2

	3		4
H2+		x2=a2 / *
	2		3

4
	H2+2x2=a2
3

4
	H2+t2=a2
3

4
	H2=a2−t2
3

	3		3
H2=		a2−		t2
	4		4

	3   3   t*√ a2− t2   4   4		3   3   √ a2t2− t4   4   4
P=		=
	2		2

	−3		3
f(t)=		t4+		a2t2
	4		4

	3
f'(t)=−3t3+		a2t
	2

	3
−3t3+		a2t=0
	2

	3
−t(3t2−		a2)=0
	2

	3
t=0 v 3t2=		a2 / * 2
	2

6t²=3a²

	a√2		a√2
t=		v t=−
	2		2

wychodzi to samo, ale źle coś, bo nie zgadza mi się po późniejszych podstawieniach tego a

salamandra: Jest ktoś w stanie znaleźć tu błąd?

Jerzy: 00:17 Skąd masz t = x√2 ? Co to jest t ?

salamandra: t to jest przerywany odcinek na rysunku ostrosłupa, 2x to krawędź podstawy, więc połowa jej to "x", więc to "t" to tak jakby przekątna kwadratu o krawędzi "x".

Jerzy: 00:56 , 5 linijka , dlaczego nie pomnożyłeś a² przez 4/3 ? i może prościej ponóż przez 2/3

salamandra:

	4
przez		aby uzyskać 2x2 i móc podstawić t2
	3

Jerzy: No ale a² nie pomnożyłeś przez 4/3

salamandra: Masz rację...

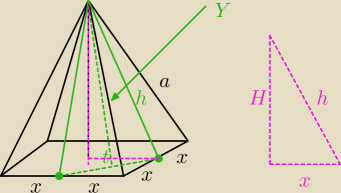salamandra: x²+h²=a² h²=a²−x² t=x√2 t²=2x

	x√2
Y2+(		)2=h2
	2

	1
Y2+		x2=h2
	2

	1
Y2+		x2=a2−x2
	2

	3		4
Y2+		x2=a2 / *
	2		3

4		4
	Y2+2x2=		a2
3		3

4		4
	Y2+t2=		a2
3		3

4		4
	Y2=		a2−t2 / * 3
3		3

4Y²=4a²−3t²

	3
Y2=a2−		t2
	4

	3   t*√a2− t2   4		3   √a2t2− t4   4
P=		=
	2		2

	3
f(t)=−		t4+a2t2
	4

f'(t)=−3t³+2a²t −3t³+2a²t=0 −t(3t²−2a²)=0 t=0 v 3t²=2a²

	2
t2=		a2
	3

	√6		−√6
t=		a v t=		a
	3		3

	√6		−√6
max dla t=		a, bo		a nie należy do dziedziny
	3		3

t=x√2

√6
	a=x√2
3

	2a√3
2x=
	3

	2a√3		12		4
Pp=(		)2=		a2=		a2
	3		9		3

H²+x²=h² H²=h²−x²

	2a√3		a√3
2x=		to x=
	3		3

	a√3		1		2
h2=a2−x2 = a2−(		)2 = a2−		a2=		a2
	3		3		3

	2		a√3		2		1		1
H2=		a2−(		)2=		a2−		a2=		a2
	3		3		3		3		3

	√3
H=		a
	3

	1		4		√3		4√3a3
V=		*		a2*		a=
	3		3		3		27

wymęczone, ale chyba teraz ok co?

Saizou : Wygląda okej

salamandra: szczerze mówiąc to nie wiem jak wpadłem na te zależności, ale obliczyłem co się dało i jakoś zlożyłem

Saizou : Czasami trzeba mieć szczęście